Home » Data Structure

Introduction to Heap Data Structure

In this article we are going to see what heap data structure is and what is its ADT operation and the implementation of heap?
Submitted by Radib Kar, on September 15, 2020

Prerequisite: Complete binary tree

What is Heap?

Heap is a complete binary tree having the below properties:

1. Each parent is either greater than its children (max heap) or less than its children (min heap)
2. It's a complete binary tree, that means all leaf nodes are either at h or h-1 (Provided h be the height of the tree) level and if the last level is not full, then the leaf nodes are as far left as possible.

Below are few examples where the tree is heap or not.

Example1:

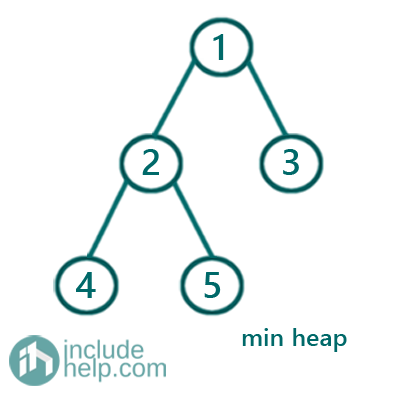
The above example is a heap and since each parent is smaller than its children, thus it's a min heap.

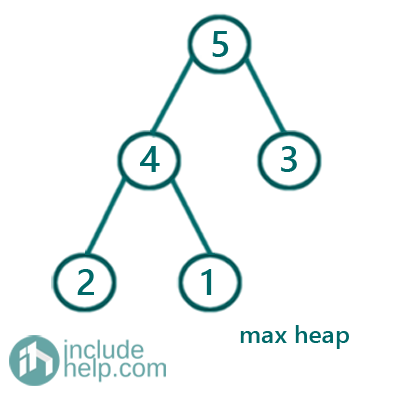
The above example is a heap and since each parent is greater than its children, thus it's a max heap.

Example3:

The above example is not a heap since for the parent 4, it has one child having value greater than it and another having value less than it. So that violates the heap property.

Type of Heaps

1. Min Heap:
   In the min heap, parent is smaller than its children. Example 1
2. Max heap:
   In the min heap, parent is greater than its children. Example 2

Heap ADT operations

1. Insert (key): Insert keys to the heap and does heapify to maintain the heap property
2. GetMin/GetMax: Returns the root of the heap which is minimum in case of min heap and maximum in case of max heap.
3. ExtractMin/ExtractMax: Remove & return the root of the heap which is minimum in case of min heap and maximum in case of max heap.

Implementation

1) Using 1D array:

This is called binary heap where we have an array arr to store the elements. Below is the heap storing information.

1. Root is arr[0]
2. To find parent of a child, parent of child arr[i] would be arr[(i-1)/2] where i>0
3. To find left child of a parent, left child of parent arr[i] would be arr[2*i+1]
4. To find left child of a parent, left child of parent arr[i] would be arr[2*i+2]

So, if we represent the example1 as binary heap, then it will be:

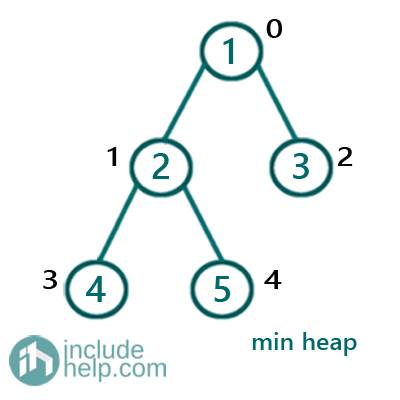
Array arr

2) Using priority_queue:

Priority queue is in another implementation for heap where priority is the heap element values.

Application of Heap

1. Data compression, huffman coding
2. Shortest path algorithm, Dijkstra's algorithm
3. Minimum Spanning tree (Prim's Algorithm)
4. Finding kth maximum/ kth minimum