Home » Data Structure

Construct a Binary Tree from Postorder and Inorder Traversal

In this article, we are going to see, how to construct a binary tree from its postorder & inorder traversals?
Submitted by Radib Kar, on August 05, 2020

In the earlier article (Traversal from which we can construct the tree), we saw that if we are given inorder traversal and any other traversal of the given tree, we can construct the tree from those two traversals. Also, in the last tutorial, we find how to construct the tree from its inorder & preorder traversal.

In the inorder traversal, we first store the left subtree then the root and finally the right subtree.

Where in the postorder traversal, we first store the left subtree root, then the right subtree and then finally the root.

Let's just assume we are given with the postorder traversal only. Can we build the tree only from postorder traversal?

Of course no. Because, though we find the root as the last element in the postorder traversal, we can't find its subtrees from the rest of the traversal.

For example, say the postorder traversal is:

2 6 4 5 3 1

We know that root of the tree is 1

But we have no idea about which part is left subtree and which part is right subtree. But for sure [2, 6, 4, 5, 3] is the traversal for the subtrees and maybe starting few elements or no elements fall in the left subtree and rest in the right subtree. So, we can't draw the partition b/w the subtrees. For this purpose, the inorder traversal helps. Because, in order traversal, if we find the root, then it's guaranteed that whichever lies before the root, falls in its left subtree & whichever lies after the root, falls in its right subtree.

Like the inorder traversal of the tree which has the previous postorder traversal is:

2 1 6 4 3 5

Here, we know that tree root is 1(we came to know from the postorder traversal of course). So it's guaranteed that [2] falls in its left subtree & [6, 4, 3, 5] falls in its right tree.

So till now what we have is shown below:

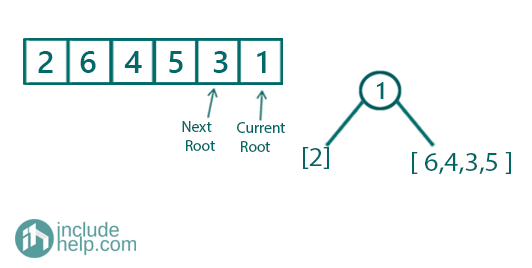
Figure 1:First Step

So the root is formed as a node. We know what part of array its left subtree and what part of the array is its right subtree.

Now we will build the subtrees recursively. In the postorder traversal, we see that after the root we have its right subtree and then its left subtree(if we start from the end and keep moving towards the start). So, here we build the right subtree first and then the left subtree. To build the right subtree we will do the same. We will have the root which is just the next element in the postorder traversal (so root is 3 now which will be the root of the right subtree).

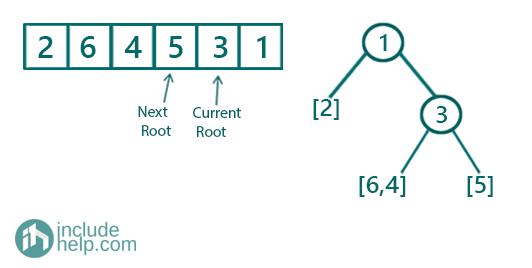
Figure 2: Second step

Now to build this right subtree,

we will do the same again. We will have the root which is just the next element in the preorder traversal (so root is 5 now). Similarly, we will search for 5 in the inorder traversal range.

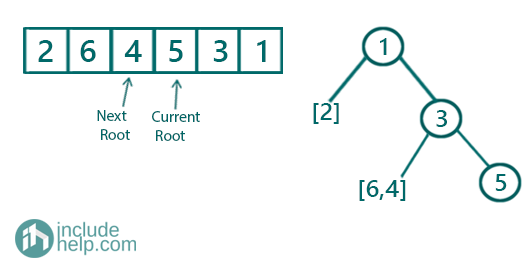
Figure 3: Step 3

Further recursions:

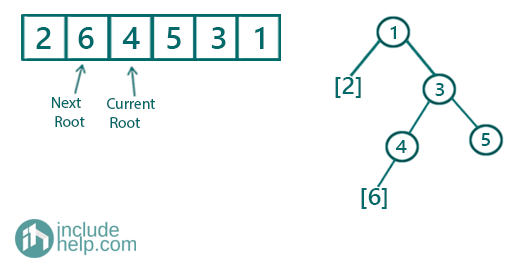
Figure 4: Step 4

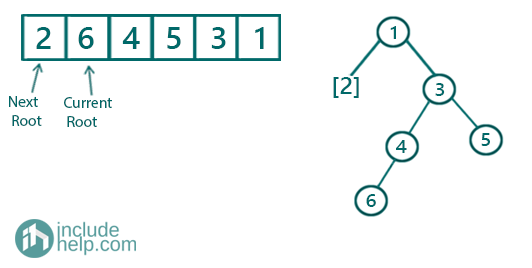
Figure 5: Step 5

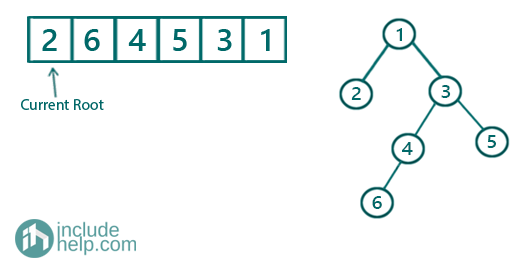
Figure 6: Step 6

The final built tree is:

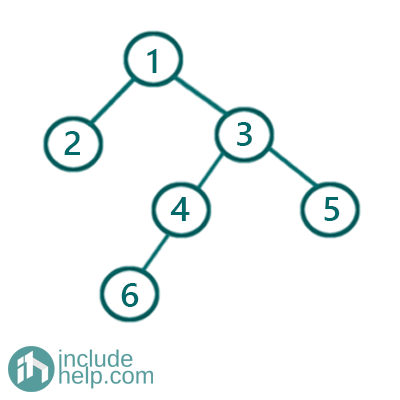
Figure 7: Final constructed Tree

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

//Searching the root position in the inorder traversal
int search(vector<int> a, int k)
{

    for (int i = 0; i < a.size(); i++)
        if (a[i] == k)
            return i;

    return -1;
}

TreeNode* buildTreeRecur(int& index, int left, int right, vector<int>& inorder, vector<int>& postorder)
{
    //base case
    if (left > right)
        return NULL;
    if (index < 0)
        return NULL;
    //search the root position in the inorder traversal
    int pivot = search(inorder, postorder[index]);
    //decrement index for next root
    index--;
    //create the root
    TreeNode* root = new TreeNode(inorder[pivot]);

    //build the right subtree recursively
    root->right = buildTreeRecur(index, pivot + 1, right, inorder, postorder);
    //build the left subtree recursively
    root->left = buildTreeRecur(index, left, pivot - 1, inorder, postorder);

    return root;
}

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
    int index = postorder.size() - 1;
    int l = 0, r = inorder.size() - 1;
    return buildTreeRecur(index, l, r, inorder, postorder);
}

//do a level order traversal
void levelOrder(TreeNode* root)
{
    queue<TreeNode*> q;
 
    q.push(root);
    q.push(NULL);
 
    int count = 0;
    while (!q.empty()) {
        TreeNode* temp = q.front();
        q.pop();
        if (!temp) {
            cout << "\nEnd of level: " << count << endl;
            count++;
            if (!q.empty()) {
                q.push(NULL);
            }
        }
        else {
            cout << temp->val << " ";
            if (temp->left)
                q.push(temp->left);
            if (temp->right)
                q.push(temp->right);
        }
    }
}

int main()
{
    //postorder traversal is stored in vector postorder
    //inorder traversal is stored in vector inorder
    vector<int> postorder{ 2, 6, 4, 5, 3, 1 };
    vector<int> inorder{ 2, 1, 6, 4, 3, 5 };

    //construct tree
    TreeNode* root = buildTree(inorder, postorder);

    cout << "Level order traversal of the tree built is:\n";
    levelOrder(root);

    return 0;
}

Output:

Level order traversal of the tree built is:
1
End of level: 0
2 3
End of level: 1
4 5
End of level: 2
6
End of level: 3