Home » Data Structure

Binary Tree representation (Sequential and Link)

Learn: In this article we are going to study about the representation of binary tree. What are the different representations of trees in the memory? What is linked list representation of binary tree? What is sequential representation of binary tree? Submitted by Amit Shukla, on October 06, 2017

I would like to request you to please read BINARY TREE DEFINATION AND ITS PROPERTIES to understand basics of binary trees and its different types.

Representing Binary Tree in memory

Let T be a Binary Tree. There are two ways of representing T in the memory as follow

1. Sequential Representation of Binary Tree.
2. Link Representation of Binary Tree.

1) Linked Representation of Binary Tree

Consider a Binary Tree T. T will be maintained in memory by means of a linked list representation which uses three parallel arrays; INFO, LEFT, and RIGHT pointer variable ROOT as follows. In Binary Tree each node N of T will correspond to a location k such that

1. LEFT [k] contains the location of the left child of node N.
2. INFO [k] contains the data at the node N.
3. RIGHT [k] contains the location of right child of node N.

Representation of a node:

In this representation of binary tree root will contain the location of the root R of T. If any one of the subtree is empty, then the corresponding pointer will contain the null value if the tree T itself is empty, the ROOT will contain the null value.

Example

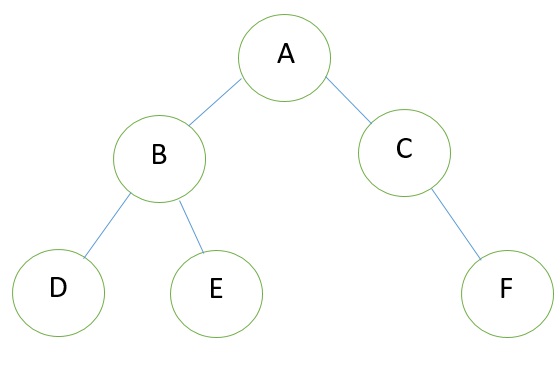
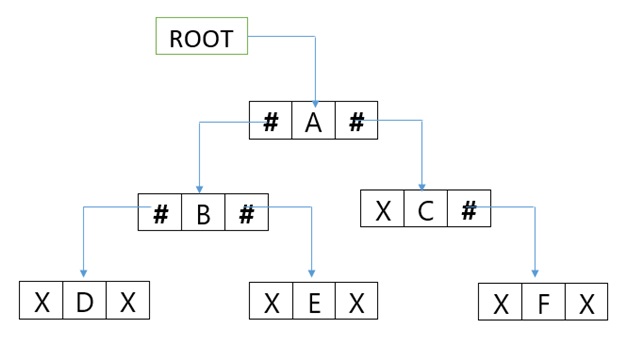
Consider the binary tree T in the figure. A schematic diagram of the linked list representation of T appears in the following figure. Observe that each node is pictured with its three fields, and that the empty subtree is pictured by using x for null entries.

Binary Tree

Linked Representation of the Binary Tree

2) Sequential representation of Binary Tree

Let us consider that we have a tree T. let our tree T is a binary tree that us complete binary tree. Then there is an efficient way of representing T in the memory called the sequential representation or array representation of T. This representation uses only a linear array TREE as follows:

1. The root N of T is stored in TREE [1].
2. If a node occupies TREE [k] then its left child is stored in TREE [2 * k] and its right child is stored into TREE [2 * k + 1].

For Example:

Consider the following Tree:

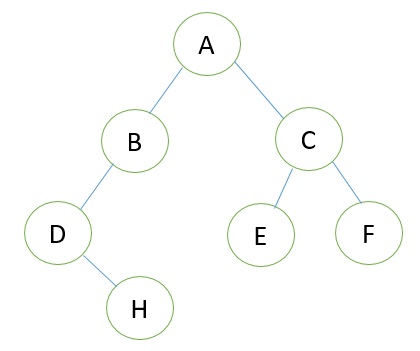
Its sequential representation is as follow: