Home » Data Structure

Tower of Hanoi using recursion (C++ program)

Implementation of Tower of HANOI in using C++ program, Learn: What is Tower of Hanoi? How to implement using recursion in C++? By Abhishek Jain Last updated : August 09, 2023

Tower of Hanoi

The Tower of Hanoi is a mathematical puzzle invented by the French mathematician Edouard Lucas in 1883.

There are three pegs, source(A), Auxiliary (B) and Destination(C). Peg A contains a set of disks stacked to resemble a tower, with the largest disk at the bottom and the smallest disk at the top. figure 1 Illustrate the initial configuration of the pegs for 3 disks. The objective is to transfer the entire tower of disks in peg A to peg C maintaining the same order of the disks.

Obeying the following rules:

1. Only one disk can be transfer at a time.
2. Each move consists of taking the upper disk from one of the peg and placing it on the top of another peg i.e. a disk can only be moved if it is the uppermost disk of the peg.
3. Never a larger disk is placed on a smaller disk during the transfer.

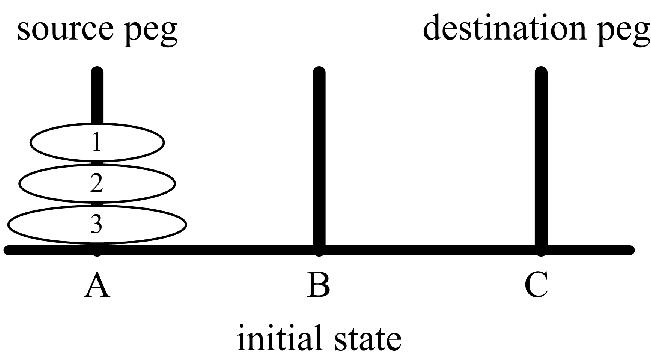
(figure 1)

The solution to the puzzle calls for an application of recursive functions and recurrence relations.

A skeletal recursive procedure (Outline) for the solution of the problem for N number of disks is as follows:

1. Move the top N-1 disks from peg A to peg B (using C as an auxiliarypeg)
2. Move the bottom disk from peg A to peg C
3. Move N-1 disks from Peg B to Peg C (using Peg A as an auxiliary peg)

The pictorial representation of the skeletal recursive procedure for N=4 disks is shown in Figure 2.

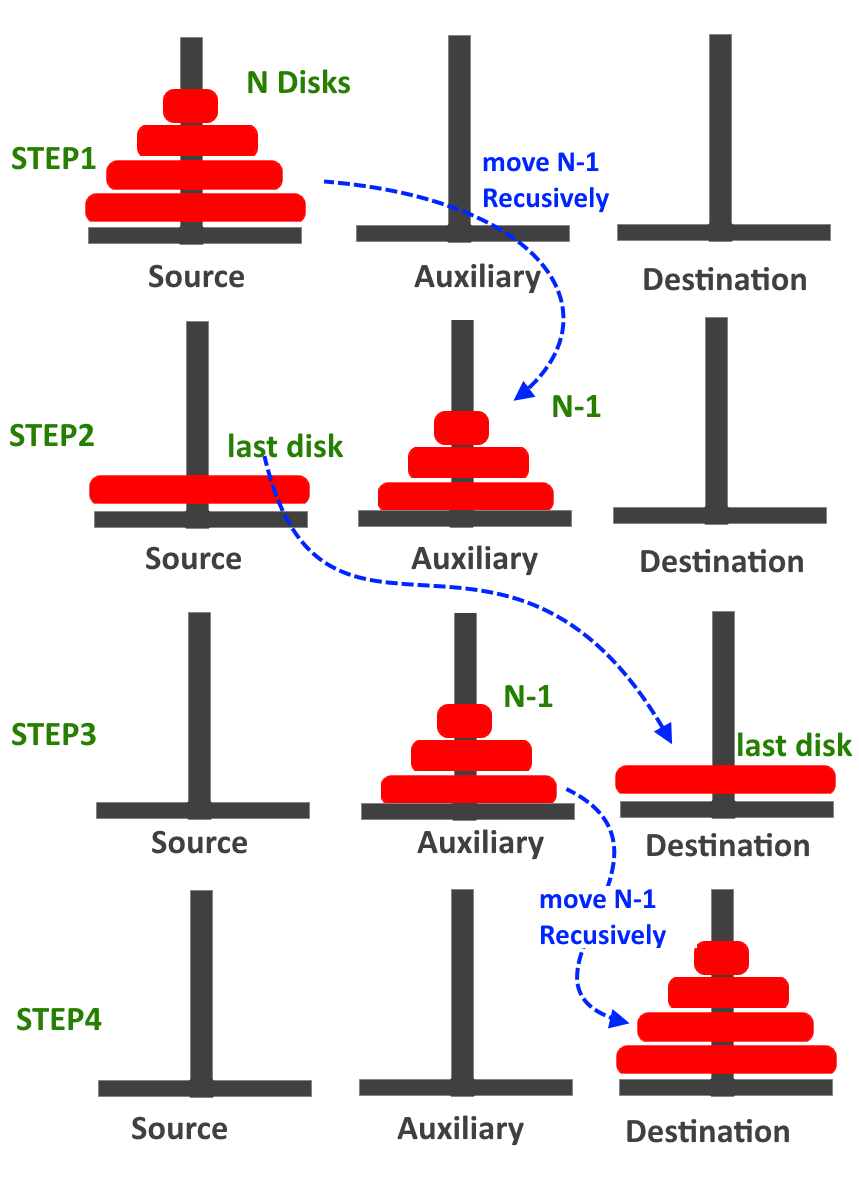
(figure 2)

Algorithm

TOH( n,  Sour, Aux , Des)
If(n=1)
    Write ("Move Disk “, n ," from ", Sour ," to ",Des)
Else
    TOH(n-1,Sour,Des,Aux);
    Write ("Move Disk “, n ," from ", Sour ," to ",Des)
    TOH(n-1,Aux,Sour,Des);
END

Let's take an example to better understand the algorithm (For n=3).

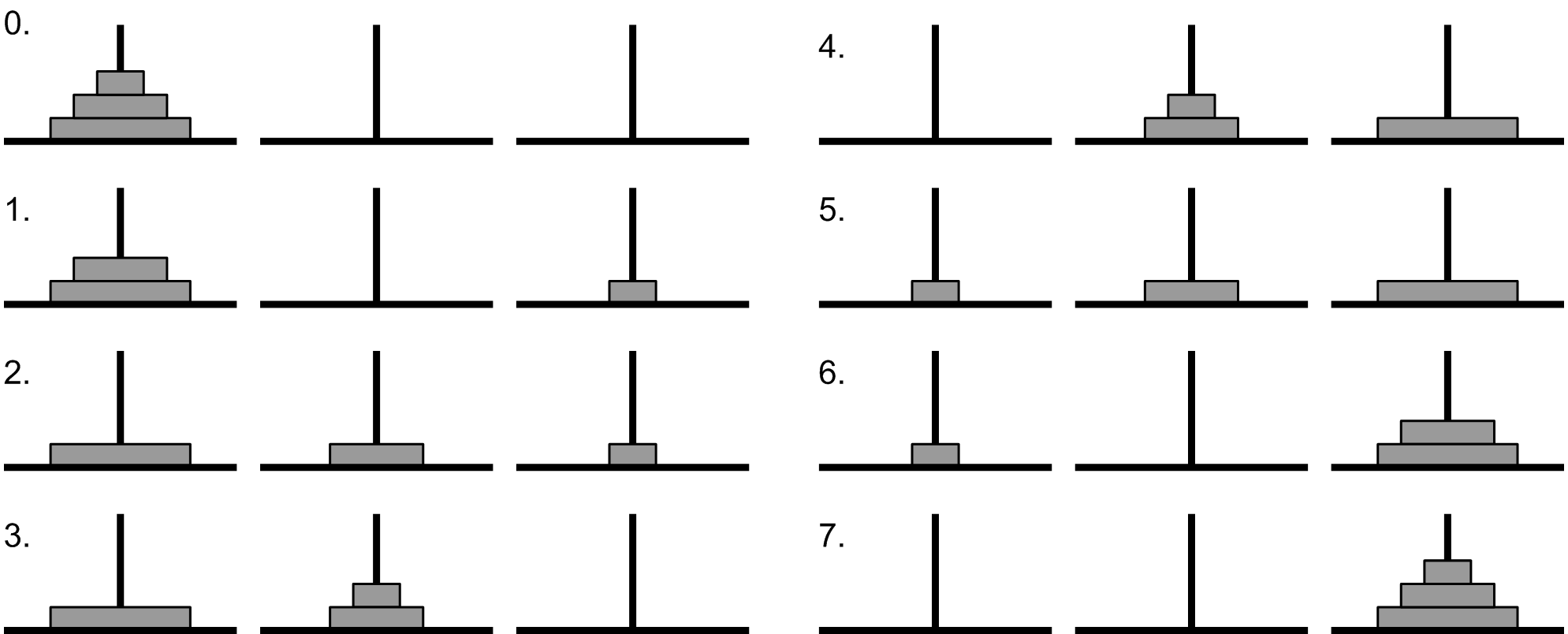
(figure 3)

Implementation of Tower of HANOI in using C++ program

#include <iostream>
using namespace std;

//tower of HANOI function implementation
void TOH(int n, char Sour, char Aux, char Des)
{
    if (n == 1) {
        cout << "Move Disk " << n << " from " << Sour << " to " << Des << endl;
        return;
    }

    TOH(n - 1, Sour, Des, Aux);
    cout << "Move Disk " << n << " from " << Sour << " to " << Des << endl;
    TOH(n - 1, Aux, Sour, Des);
}

//main program
int main()
{
    int n;

    cout << "Enter no. of disks:";
    cin >> n;
    //calling the TOH
    TOH(n, 'A', 'B', 'C');

    return 0;
}

Output

Enter no. of disks:3
Move Disk 1 from A to C
Move Disk 2 from A to B
Move Disk 1 from C to B
Move Disk 3 from A to C
Move Disk 1 from B to A
Move Disk 2 from B to C
Move Disk 1 from A to C

Image Reference:

1. Towers Of Hanoi
2. An Evolutionary Approach to Tower of Hanoi Problem