Home » Data Structure

Prim's Minimum Spanning Tree

Prim's Minimum Spanning Tree: In this article we are going to see prim's minimum spanning tree and its implementation. Submitted by Souvik Saha, on March 25, 2019

What to Learn?

How to construct minimum spanning tree using Prim's Minimum Spanning Tree algorithm and its C++ implementation?

Minimum Spanning Tree is a tree with all the vertices of the graph and who has a minimum weight.

In the figure there is a graph with 9 vertexes.

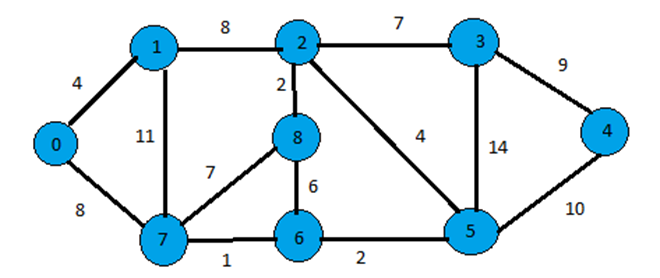
If we construct a minimum spanning tree then it would be like,

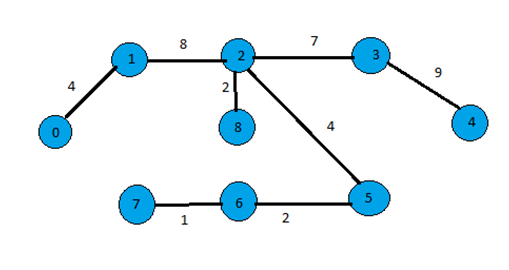
Algorithm:

To implement the Prim's Minimum Spanning Tree algorithm, we have an array of all the vertices with their corresponding distance.

1. Initially, all the vertices have a distance infinity except the starting vertex which has distance zero.
2. We check the all the unvisited reachable vertices from the starting vertex and update all the distance with weighted edge distance from that vertex.
3. Choose the minimum unvisited distance and choose the corresponding vertex.
4. Repeat step 2 and 3 until all the vertices are visited.

Example with explanation:

The above algorithm is described using an example (graph above),

We first start with vertex 0 and the array is initially.

Then look for unvisited reachable vertices with minimum distance. From vertex 0 unvisited vertices are 1 and 2 and 1 has a minimum weighted edge then it attached with vertex 0.

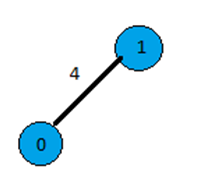
And the array is:

Then from vertex 1 unvisited reachable vertices are 2, 7 and from vertex 0 unvisited reachable vertex is 7 and both have same distance so choose any one from them.

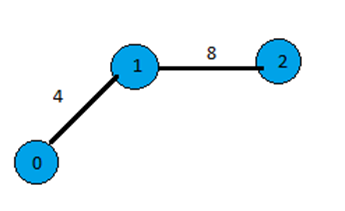
And the array is,

And finally, the spanning tree will be this...

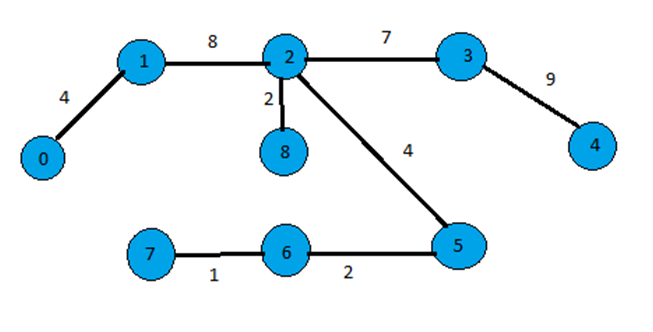
C++ implementation:

#include <bits/stdc++.h>
using namespace std;

//Make a pair between vertex x and vertex y 
//who's weighted edge is z 
void addedge(list< pair<int,int> > *ls,int x,int y,int z){
	ls[x].push_back(make_pair(y,z));	
	ls[y].push_back(make_pair(x,z));
	return;
} 
//Find the minimum value of weighted edges from unvisited 
//vertices and return the vertex
int mini(bool *visit,int num,int arr[][9]){
	int temp=INT_MAX;
	int store;
	for(int i=0;i<num;i++){
		if(!visit[i] && arr[1][i]<temp){
			temp=arr[1][i];
			store=i;
		}
	}
	return store;
}

//Prim's Minimum spanning Tree algorithm
void prims(list< pair<int,int> >*ls,list< pair<int,int> >*min_span,int num,int x){
	int arr[2][9];
	//create a matrix with the same number of 
	//vertices the graph have
	for(int i=0;i<num;i++){
		arr[0][i]=i;
		if(i==x){
			arr[1][i]=i;
		}
		else{
			arr[1][i]=INT_MAX;
		}
	}
	//create a visit array
	bool *visit=new bool[num];
	for(int i=0;i<num;i++){
		visit[i]=false;
	}
	
	int count=1;
	//while all verices are visit
	while(count<=num){
		int temp=x;
		//add to the set 
		min_span[0].push_back(make_pair(x,arr[1][x]));
		visit[x]=true;
		list<pair<int,int> >::iterator it;
		for(it=ls[temp].begin();it!=ls[temp].end();it++){
			//when not visited and distance is greater 
			//then cuuent distance 
			if(!visit[it->first] && arr[1][it->first]>it->second){
				arr[1][it->first]=it->second;
			}
		}
		//find the minimum weighted edge attached vertex
		x=mini(visit,num,arr);
		count++;
	}
	cout<<"Index with their distance"<<endl;
	for(int i=0;i<num;i++){
		cout<<arr[0][i]<<arr[1][i]<<endl; 
	}
}

// Print the Adjacency List
void print(list<pair<int,int> > *ls,int num){
	list<pair<int,int> >::iterator it;
	for(int i=0;i<9;i++){
		cout<<i<<"-->";
		for(it=ls[i].begin();it!=ls[i].end();it++){
			cout<<it->first<<" ("<<it->second<<")"<<"-->";
		}
		cout<<endl;
	}
}

int main(){
	int num=9;
	
	cout<<"Enter the no. of vertices : 9\n";
	list<pair<int,int> > ls[num];
	list<pair<int,int> > min_span[1];
	
	addedge(ls,0,1,4);
	addedge(ls,0,7,8);
	addedge(ls,1,7,11);
	addedge(ls,1,2,8);
	addedge(ls,7,6,1);
	addedge(ls,7,8,7);
	addedge(ls,2,3,7);
	addedge(ls,2,5,4);
	addedge(ls,2,8,2);
	addedge(ls,8,6,6);
	addedge(ls,6,5,2);
	addedge(ls,5,4,10);
	addedge(ls,5,3,14);
	addedge(ls,3,4,9);
	
	cout<<"Print of adjacency matrix:"<<endl;
	print(ls,9);
	prims(ls,min_span,9,0);
	
	cout<<"Path of the spanning tree"<<endl;
	list<pair<int,int> >::iterator it;
	
	for(it=min_span[0].begin();it!=min_span[0].end();it++){
		cout<<it->first<<" ("<<it->second<<")"<<"-->";
	}
	
	return 0;
}

Output

Enter the no. of vertices :9
Print of adjacency matrix:
0-->1 (4)-->7 (8) 
1-->0 (4)-->7 (11)-->2 (8) 
2-->1 (8)-->3 (7)-->5 (4)-->8 (2)
3-->2 (7)-->5 (14)-->4 (9)
4-->5 (10)-->3 (9)
5-->2 (4)-->6 (2)-->4 (10)-->3 (14)
6-->7 (1)-->8 (6)-->5 (2)
7-->0 (8)-->1 (11)-->6 (1)-->8 (7)
8-->7 (7)-->2 (2)-->6 (6)
Index with their distance
0 0
1 4
2 8
3 7
4 9
5 4
6 2
7 1
8 2
Path of the spanning tree
0 (0)-->1 (4)-->2 (8)-->8 (2)-->5 (4)-->6 (2)-->7 (1)-->3 (7)-->4 (9)