Home » Data Structure

Traversal technique for Binary Tree

Learn: In this article, we will learn about Traversal technique for Binary tree with their algorithms and example. Submitted by Abhishek Kataria, on June 11, 2018

Binary Tree

A binary tree is a finite collection of elements or it can be said it is made up of nodes. Where each node contains the left pointer, right pointer, and a data element. The root pointer points to the topmost node in the tree. When the binary tree is not empty, so it will have a root element and the remaining elements are partitioned into two binary trees which are called the left pointer and right pointer of a tree.

Traversing in the Binary Tree

Tree traversal is the process of visiting each node in the tree exactly once. Visiting each node in a graph should be done in a systematic manner. If search result in a visit to all the vertices, it is called a traversal. There are basically three traversal techniques for a binary tree that are,

1. Preorder traversal
2. Inorder traversal
3. Postorder traversal

1) Preorder traversal

To traverse a binary tree in preorder, following operations are carried out:

1. Visit the root.
2. Traverse the left sub tree of root.
3. Traverse the right sub tree of root.

Note: Preorder traversal is also known as NLR traversal.

Algorithm:

Algorithm preorder(t)
/*t is a binary tree. Each node of t has three fields: 
lchild, data, and rchild.*/
{
	If t! =0 then
	{
		Visit(t);
		Preorder(t->lchild);
		Preorder(t->rchild);
	}
}

Example: Let us consider the given binary tree,

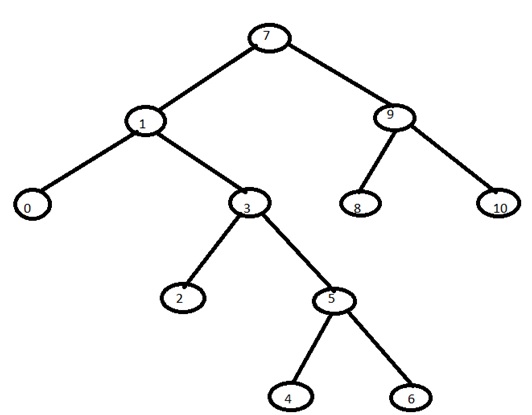
Therefore, the preorder traversal of the above tree will be: 7,1,0,3,2,5,4,6,9,8,10

2) Inorder traversal

To traverse a binary tree in inorder traversal, following operations are carried out:

1. Traverse the left most sub tree.
2. Visit the root.
3. Traverse the right most sub tree.

Note: Inorder traversal is also known as LNR traversal.

Algorithm:

Algorithm inorder(t)

/*t is a binary tree. Each node of t has three fields: 
lchild, data, and rchild.*/
{
	If t! =0 then
	{
		Inorder(t->lchild);
		Visit(t);
		Inorder(t->rchild);
	}
}

Example: Let us consider a given binary tree.

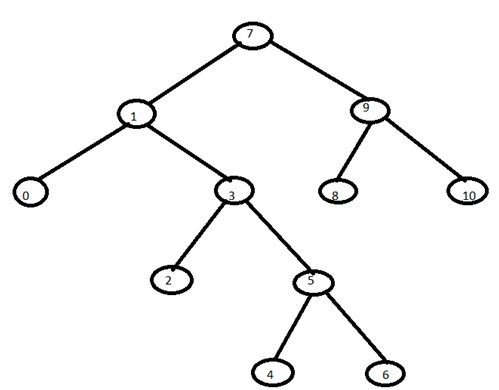
Therefore the inorder traversal of above tree will be: 0,1,2,3,4,5,6,7,8,9,10

3) Postorder traversal

To traverse a binary tree in postorder traversal, following operations are carried out:

1. Traverse the left sub tree of root.
2. Traverse the right sub tree of root.
3. Visit the root.

Note: Postorder traversal is also known as LRN traversal.

Algorithm:

Algorithm postorder(t)

/*t is a binary tree .Each node of t has three fields: 
lchild, data, and rchild.*/
{
	If t! =0 then
	{
		Postorder(t->lchild);
		Postorder(t->rchild);
		Visit(t);
	}
}

Example: Let us consider a given binary tree.

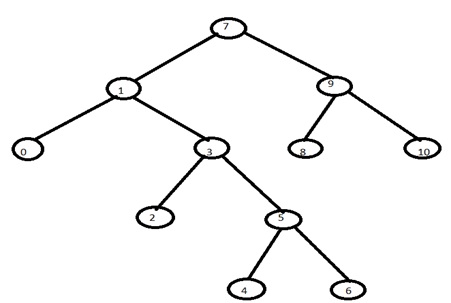
Therefore the postorder traversal of the above tree will be: 0,2,4,6,5,3,1,8,10,9,7