Home » Data Structure

Level Order Traversal on a Binary Tree | Data Structure

In this article, we are going to learn Level order traversal on a binary tree: Inorder, Preorder and Postorder Traversal.
Submitted by Radib Kar, on September 29, 2018

For traversal on any binary tree, we mainly use three types of traversal. Those are:

1. Inorder traversal
2. Preorder Traversal
3. Postorder Traversal

But there is another kind of traversal technique, quite similar to BFS of the graph, known as "Level order traversal".

The level order traversal means traversing left to right level-wise. Level order traversal of the following example turns to be: 2, 7, 5, 2, 6, 9, 5, 11, 4.

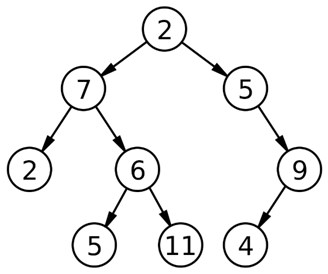
Image source: Wikipedia

The level order traversal is defined as follows:

• Visit the root
• While traversing level l, keep all elements at level l+1 in queue
• Go to next level and visit all the nodes at that level
• Repeat until all levels are completed

Additional data structure used: Queue

Pseudocode:

struct BT{              // tree node type
	int data;           //value
	struct BT *left;    //pointer to left child
	struct BT *right;   //pointer to right child
};


void levelorder (struct BT *root){ // root of the tree
	struct BT *temp;                // BT refers to node of tree (datatype for the node);
	struct Queue *q=Creat_queue();  //creating a queue
	
	if(!root)   //root is null
	return;
	
	EnQueue(q,root); // Enqueue the root in the queue
		
	while(!emptyQueue(q)){
		temp=DeQueue(q);  //Dequeue
		print(temp->data); //print the data
		if(temp->left)
			EnQueue(q,temp->left); // if left child exists EnQueue
		if(temp->right)
			EnQueue(q,temp->right); // if right child exists EnQueue
	}
	DeleteQueue(q);
}

C++ implementation of level order traversal

#include <bits/stdc++.h>
using namespace std;

class tree{    // tree node is defined
	public:
	int data;
	tree *left;
	tree *right;
};

void levelorder( tree *root){
	queue<tree*> q;  // using stl
	tree* temp;
	q.push(root);
	while(!q.empty()){
		temp=q.front();
		q.pop();
		cout<<temp->data<<" ";  //process node
		if(temp->left)
			q.push(temp->left); //EnQueue
		if(temp->right)
			q.push(temp->right); //EnQueue
	}
}
tree* newnode(int data)  // creating new node
{ 
    tree* node = (tree*)malloc(sizeof(tree)); 
    node->data = data; 
    node->left = NULL; 
    node->right = NULL; 
  
    return(node); 
} 
  

int main() 
{ 
    //**same tree is builted as shown in example**
    tree *root=newnode(2); 
    root->left= newnode(7); 
    root->right= newnode(5); 
    root->right->right=newnode(9);
    root->right->right->left=newnode(4);
    root->left->left=newnode(2); 
    root->left->right=newnode(6);
    root->left->right->left=newnode(5);
    root->left->right->right=newnode(11);
  
    cout<<"Level Order traversal of binary tree is :"<<endl; 
    levelorder(root); 
  
    return 0; 
}

Output

Level Order traversal of binary tree is :
2 7 5 2 6 9 5 11 4