Home » Data Structure

Kth Minimum in a Binary Search Tree

In this article, we are going to see how to find Kth minimum in a Binary Search Tree?
Submitted by Radib Kar, on October 30, 2020

As we have discussed in our introductory article on Binary search tree, that finding kth minimum is an ADT operation. Here, we are going to see how we can find kth minimum in a given binary search tree.

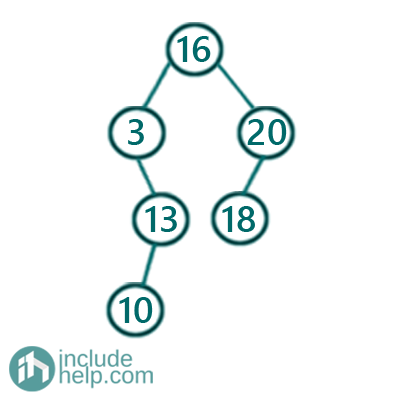
In the above binary search tree, the 3rd minimum is 13 and the 5th minimum is 18

So how can we find kth minimum given the binary search tree and the k as input?

The idea is inorder traversal. If we do the inorder traversal then we will reach to the minimum node in the BST first. So, we need to keep a counter which will increment to find the kth minimum only. The inorder traversal visits the BST nodes in sorted order(ascending). So it will visit the 1^st minimum first, then the 2^nd minimum and so on. So, our counter will determine the kth minimum. So the reverse order traversal is like below,

void kthSmallestRec(TreeNode* root,int K,int &count,int &ans){
    if(!root)
        return;
    //reach the 1st minimum node first doing inorder traversal
    kthSmallestRec(root->left,K,count,ans);
    //increment count
    count++;
    if(count==K){//if it's K then the current node value is kth minimum
        ans=root->val;
        return;
    }    
    kthSmallestRec(root->right,K,count,ans);    
}

Below is the visual illustration on how we find the kth minimum

Say k=3

And the given BST is the same as example

So, doing the inorder traversal first we reach the minimum node. To show how-

First, we start from the root node

Then it goes to the immediate left child 3 and then the further left child is NULL, so control comes back to this node 3 and that's our first minimum. Counter is now 1

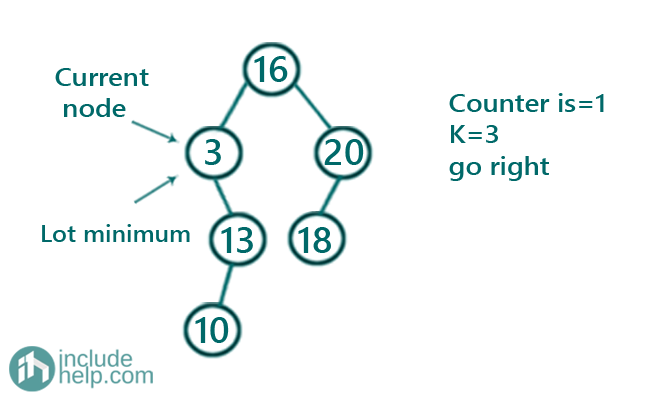
Since the counter is not K, so it will recur for its right subtree

Now the current node is 13 and since there is left subtree so it will go there. Thus the current Node is 10 and since it has no left subtree, so control comes back to this node and this is our 2^nd minimum as counter is 2 now.

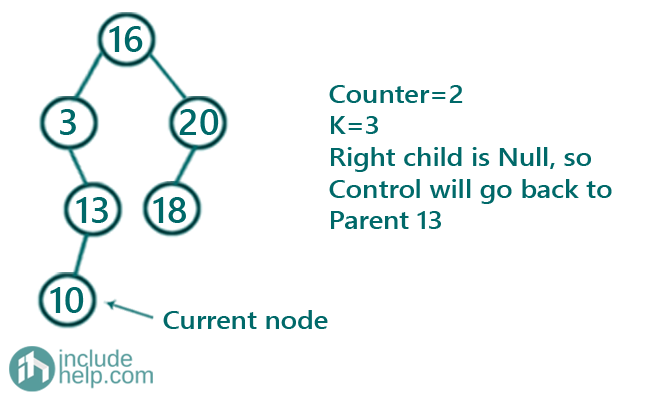
Now it will recur for the right subtree but since there is no right subtree the control will reach back to its parent 13. So counter is 3 and that’s why 13 our 3rd minimum.

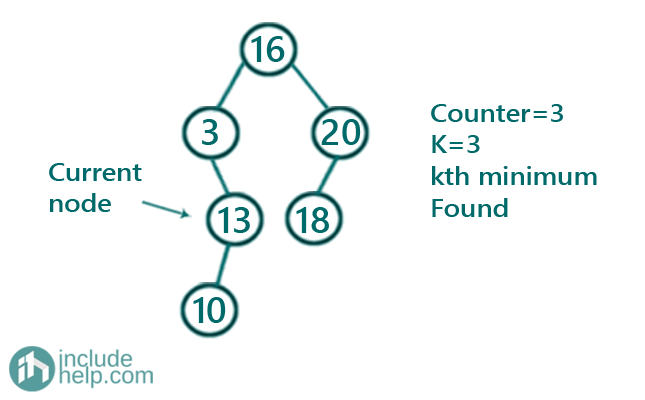
If we extend this to find 5^th minimum, we can do a similar way and will find that 18 is our 5^th minimum.

Below is the C+++ implementation of the above idea.

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

//inorder traversal to find kth minimum element
void kthSmallestRec(TreeNode* root, int K, int& count, int& ans)
{
    if (!root)
        return;
    //reach the 1st minimum node fisrt doing inorder traversal
    kthSmallestRec(root->left, K, count, ans);
    //increment count
    count++;
    if (count == K) { //if it's K then the current node value is kth minimum
        ans = root->val;
        return;
    }

    kthSmallestRec(root->right, K, count, ans);
}

// return the Kth minimum element in the given BST rooted at root
int kthSmallest(TreeNode* root, int K)
{
    //Your code here
    int ans = INT_MIN;
    int count = 0;
    kthSmallestRec(root, K, count, ans);

    return ans;
}

int main()
{
    TreeNode* root = new TreeNode(16);
    root->left = new TreeNode(3);
    root->left->right = new TreeNode(13);
    root->left->right->left = new TreeNode(10);
    root->right = new TreeNode(20);
    root->right->left = new TreeNode(18);
    int k = 3;
    cout << "3rd minimum is: " << kthSmallest(root, k) << endl;
    k = 5;
    cout << "5th minimum is: " << kthSmallest(root, k) << endl;
    return 0;
}

Output:

3rd minimum is: 13
5th minimum is: 18