Home » Algorithms

Radix Sort Algorithm: What It Is, Time Complexity, Example, Advantages & Disadvantages

Radix Sort Algorithm: In this tutorial, we will learn about the radix sort, its time complexity, examples, advantaged, and disadvantages. By Prerana Jain Last updated : August 12, 2023

Radix Sort

Radix sort is based on a linear sorting algorithm which is useful for sorting integers or strings with fixed-size keys. Radix sort uses the technique of sorting the elements digit by digit. It is an efficient sorting algorithm for integers or strings with fixed-size keys. Radix sort has also been called bucket sort and digital sort. In other words, we can say that Radix sort is a method that can be used to sort a list of a number by its base. If we want to sort the list of English words, where radix or base is 26 then 26 buckets are used to sort the words.

To sort an array of decimal number where the radix or base is 10 we need 10 buckets and can be numbered as 0,1,2,3,4,5,6,7,8,9. A number of passes required to have a sorted array depend upon the number of digits in the largest element.

Radix Sort Algorithm

The following are the steps with an example of implementing the Radix sort:

Let A be a linear array of n elements A[1], A[2], A[3], ..., A[n]. Digit is the total number of digit in the largest element in array A.

1. Input n number of elements in an array A.
2. Find the total number of digits in the largest element in the array.
3. Initialize i=1 and repeat the steps 4 and 5 until( i<=Digit).
4. Initialize the bucket j=0 and repeat the steps 5until (j<n).
5. Compare the i^th position of each element of the array with bucket number and place it in the corresponding bucket.
6. Read the elements (S) of the bucket from 0^th bucket to 9^th bucket and from the first position to the higher one to generate new array A.
7. Display the sorted array A.
8. Exit.

Radix Sort Time Complexity

Time requirement for the radix sorting method depends on the number of digits and the elements in the array. Suppose A is an array of n elements A1, A2... An and let r denote the radix( for example r=10 for decimal digits, r=26 for English letters and r=2 for hits). If A1 is the largest number then A! Can be represented. Then radix sort require s passes. In passes, each element is compared with the bucket elements.

So the radix sort requires the total comparison f(n) of: F(n) < = r x s x n

Worst case

In the worst case s = n so F(n) = O(n2)

Best case

In the best case s = logn so f(n) = (nlogn)

Average case

It is very hard to define the time complexity. Because it will depend on the choice of the radix r and also the number of a digit on largest elements (i.e number of passes) but on an average (log n) comparison is required so f(n) = O(nlogn)

Advantages of Radix Sort

The following are the advantages of radix sort:

1. It is implemented in Java, it would be faster than quicksort or heap.
2. It is stable because it preserves existing order of equals keys.
3. It is good on small keys.

Disadvantages of Radix Sort

The following are the disadvantages of radix sort:

1. It is not efficient on very long keys because the total sorting time is proportional to key length and to the number of items to sort.
2. We have to write an unconventional compare routine.
3. It requires fixed size keys and some standard way of breaking the keys to pieces.

Radix Sort Example

To illustrate the radix sort consider the following array with 7 elements

42, 133, 7, 23, 74, 670, 49

In this array, the biggest elements are 670 and the number of digits is 3, so 3 passes are required to sort the array. Read the elements and compare the first position (2 is in the first position of 42) digits with the digits of the buckets and place it

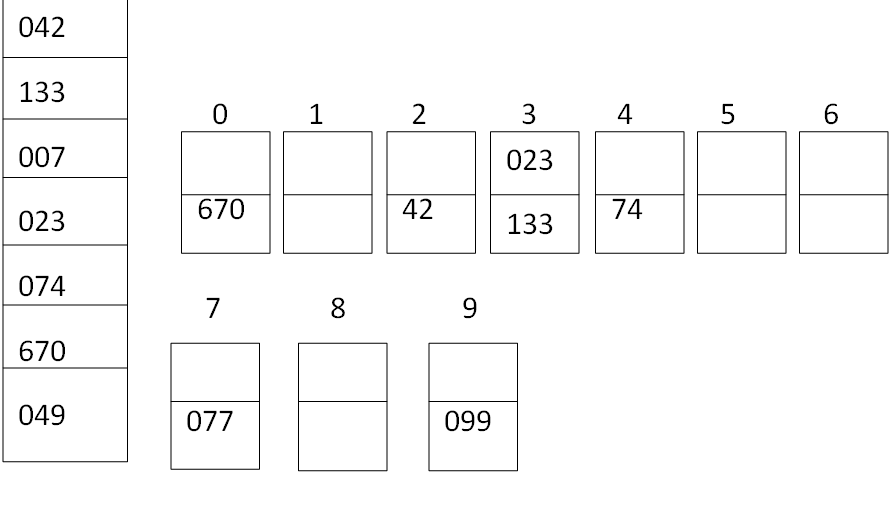
Now read the elements from left to right and the bottom to the top of the bucket and place it in an array for the next pass. Read the array elements and compare the second position (4 is in the second position of the elements 042) digit with a number of the bucket and place it.

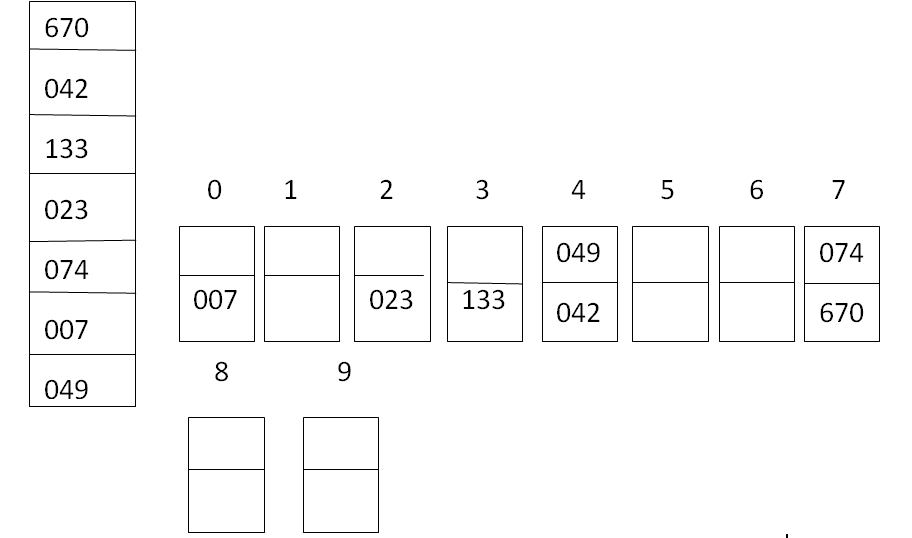
Again read the element from left to right and from bottom to top to get an array for the third pass. (0 is in the first position of 042) compare the third position digit in each element with the budget digit and place it wherever it matches.

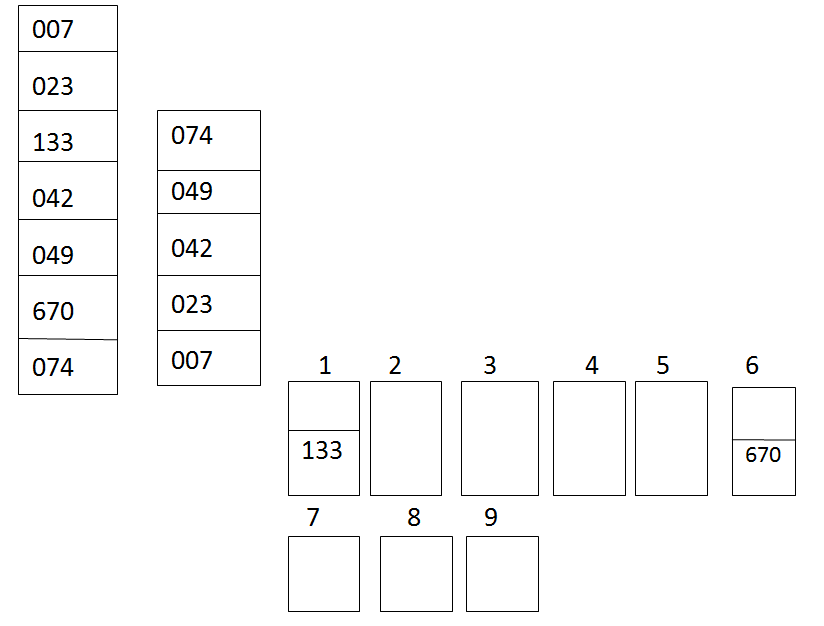
Now the sorted array is 7 , 23, 42, 49, 74, 133, 670.