Home »
Algorithms
Optimal Merge Pattern (Algorithm and Example)
Algorithms | Optimal Merge Pattern: In this tutorial, we will learn about the optimal merge pattern with its algorithm and an example.
By Shivangi Jain Last updated : August 16, 2023
Optimal Merge Pattern
Optimal merge pattern is a pattern that relates to the merging of two or more sorted files in a single sorted file. This type of merging can be done by the two-way merging method.
If we have two sorted files containing n and m records respectively then they could be merged together, to obtain one sorted file in time O (n+m).
There are many ways in which pairwise merge can be done to get a single sorted file. Different pairings require a different amount of computing time.The main thing is to pairwise merge the n sorted files so that the number of comparisons will be less.
The formula of external merging cost is:
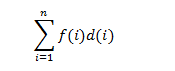
Where, f (i) represents the number of records in each file and d (i) represents the depth.
Pseudo code for optimal merge pattern
Algorithm Tree(n)
//list is a global list of n single node
{
For i=1 to i= n-1 do
{
// get a new tree node
Pt: new treenode;
// merge two trees with smallest length
(Pt = lchild) = least(list);
(Pt = rchild) = least(list);
(Pt =weight) = ((Pt = lchild) = weight) = ((Pt = rchild) = weight);
Insert (list , Pt);
}
// tree left in list
Return least(list);
}
How optimal merge pattern works?
An optimal merge pattern corresponds to a binary merge tree with minimum weighted external path length. The function tree algorithm uses the greedy rule to get a two- way merge tree for n files. The algorithm contains an input list of n trees. There are three field child, rchild, and weight in each node of the tree. Initially, each tree in a list contains just one node. This external node has lchild and rchild field zero whereas weight is the length of one of the n files to be merged. For any tree in the list with root node t, t = it represents the weight that gives the length of the merged file. There are two functions least (list) and insert (list, t) in a function tree. Least (list) obtains a tree in lists whose root has the least weight and return a pointer to this tree. This tree is deleted from the list. Function insert (list, t) inserts the tree with root t into the list.
The main for loop in this algorithm is executed in n-1 times. If the list is kept in increasing order according to the weight value in the roots, then least (list) needs only O(1) time and insert (list, t) can be performed in O(n) time. Hence, the total time taken is O (n2). If the list is represented as a minheap in which the root value is less than or equal to the values of its children, then least (list) and insert (list, t) can be done in O (log n) time. In this condition, the computing time for the tree is O (n log n).
Optimal merge pattern example
Given a set of unsorted files: 5, 3, 2, 7, 9, 13
Now, arrange these elements in ascending order: 2, 3, 5, 7, 9, 13
After this, pick two smallest numbers and repeat this until we left with only one number.
Now follow following steps:
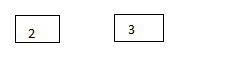
Step 1: Insert 2, 3
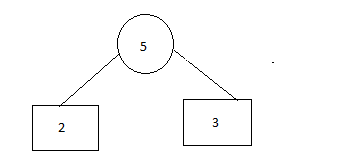
Step 2:
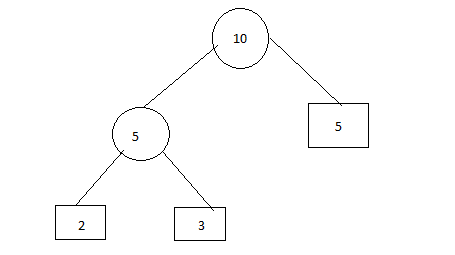
Step 3: Insert 5
Step 4: Insert 13
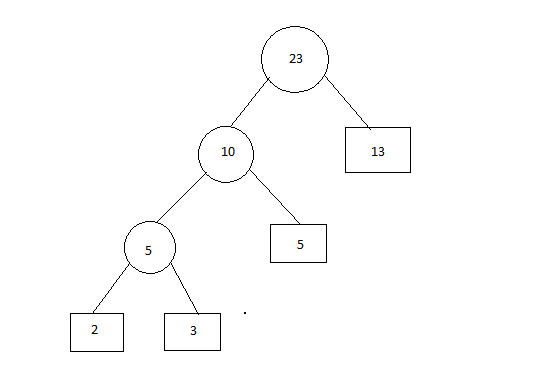
Step 5: Insert 7 and 9
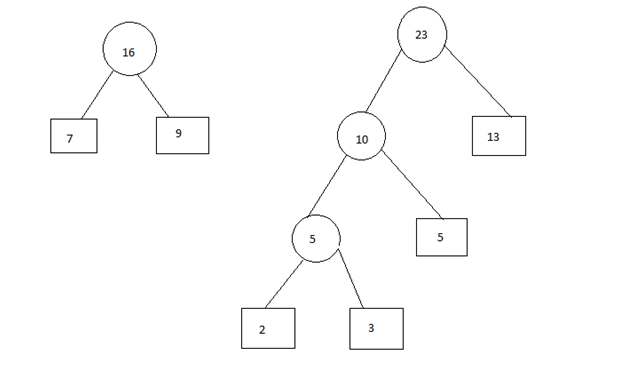
Step 6:
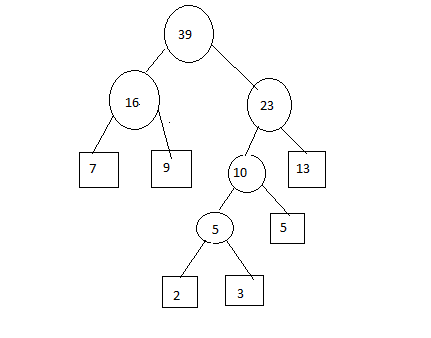
So, The merging cost = 5 + 10 + 16 + 23 + 39 = 93
Advertisement
Advertisement