Home »
Algorithms
Reliability design problem
In this article, we will learn about the concept of reliability design problem.
Submitted by Shivangi Jain, on August 21, 2018
Reliability design problem
In reliability design, the problem is to design a system that is composed of several devices connected in series.

If we imagine that r1 is the reliability of the device.
Then the reliability of the function can be given by πr1.
If r1 = 0.99 and n = 10 that n devices are set in a series, 1 <= i <= 10, then reliability of the whole system πri can be given as: Πri = 0.904
So, if we duplicate the devices at each stage then the reliability of the system can be increased.
It can be said that multiple copies of the same device type are connected in parallel through the use of switching circuits. Here, switching circuit determines which devices in any given group are functioning properly. Then they make use of such devices at each stage, that result is increase in reliability at each stage. If at each stage, there are mi similar types of devices Di, then the probability that all mi have a malfunction is (1 - ri)^mi, which is very less.
And the reliability of the stage I becomes (1 – (1 - ri) ^mi). Thus, if ri = 0.99 and mi = 2, then the stage reliability becomes 0.9999 which is almost equal to 1. Which is much better than that of the previous case or we can say the reliability is little less than 1 - (1 - ri) ^mi because of less reliability of switching circuits.
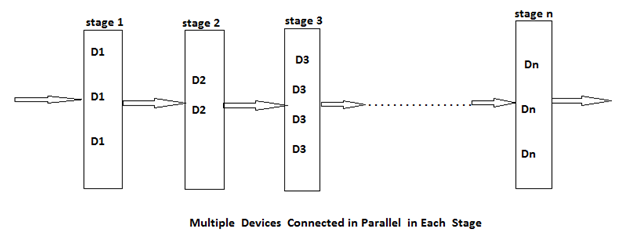
In reliability design, we try to use device duplication to maximize reliability. But this maximization should be considered along with the cost.
Let c is the maximum allowable cost and ci be the cost of each unit of device i. Then the maximization problem can be given as follows:
Maximize π Øi (mi) for 1 <= I <= n
Subject to:
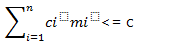
mi>= 1 and integer 1 <= i <= n
Here, Øi (mi) denotes the reliability of the stage i.
The reliability of the system can be given as follows:
Π Øi (mi) for 1 <= i <= n
If we increase the number of devices at any stage beyond the certain limit, then also only the cost will increase but the reliability could not increase.
Advertisement
Advertisement