Home » Algorithms

Insertion Sort Algorithm: What It is, Flow Chart, Time Complexity, and Implementation

Insertion Sort Algorithm: In this tutorial, we will learn about insertion sort, its algorithm, flow chart, and its implementation using C, C++, and Python. By Raunak Goswami Last updated : August 12, 2023

In the last article, we discussed about the bubble sort with algorithm, flowchart and code. In this article, we are going to discuss about another basic sorting technique i.e. insertion sort.

Insertion Sort Algorithm

As the name suggests the sorting is done by using successive insertions of the key element selected by the sorting algorithm at its correct place. As the sorting begins the key element chosen is always the second element so that there can be at least one element at the left of the key element to be compared. After comparison the key element is swapped with the element at its left if required and the key element is changed to the element at the immediate right of the previous key element after that the key element is again compared with the elements at it left and the element is swapped with the key element after comparison if required, if the sorting is done in ascending order then the key element should always be greater than the element at its left if not, then the swapping is performed with key element and vice versa for the descending order.

Insertion Sort Algorithm Pseudo Code

Let us look at the algorithm of insertion sort for a better understanding of the logic to be used:

Insertion sort(a[],n)
for j->2 to n
    do key <-a[j]
    i<-j-1
    while i>=0 and a[i]>key
        do a[i+1]<-a[i]
        i<-i+1
    a[i+1]<-key
end

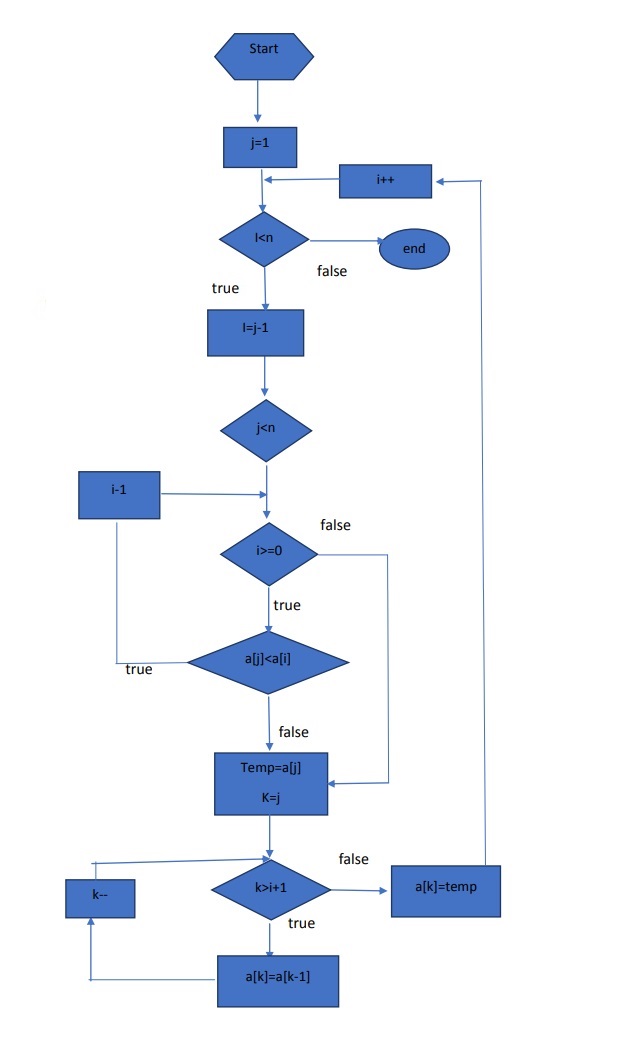
Insertion Sort Algorithm Flow chart

The insertion algorithm can also be explained in the form of a flowchart as follows:

Insertion Sort Using C

The below is the implementation of insertion sort using C program:

#include <stdio.h>

int main()
{
    int a[6];
    int key;
    int i, j;
    int temp;

    printf("Enter any six elements to be sorted using insertion sort\n");
    for (i = 0; i < 6; i++) {
        scanf("%d", &a[i]);
    }

    for (j = 1; j < 6; j++) {
        key = a[j];
        i = j - 1;
        while ((i >= 0) && (a[i] >= key)) {
            temp = a[i + 1];
            a[i + 1] = a[i];
            a[i] = temp;
            i = i - 1;
        }
        a[i + 1] = key;
    }

    printf("elements after sorting using insertion sort are \n");
    for (i = 0; i < 6; i++) {
        printf("%d  \n", a[i]);
    }

    return 0;
}

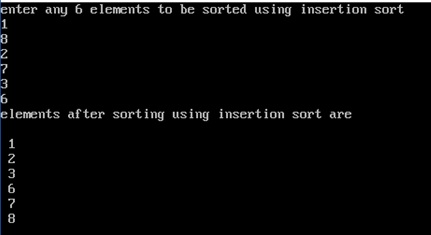
The output of the above program will be:

Insertion Sort Using C++

The below is the implementation of insertion sort using C++ program:

#include <iostream>
using namespace std;

int main()
{
    int key, i, j, temp;
    int c, a[100];

    cout << "enter the no of elements you want to enter" << endl;
    cin >> c;

    cout << "Enter the elements" << endl;
    for (i = 0; i < c; i++) {
        cin >> a[i];
    }

    for (j = 1; j < c; j++) {
        key = a[j];
        i = j - 1;
        while ((i >= 0) && (a[i] >= key)) {
            temp = a[i + 1];
            a[i + 1] = a[i];
            a[i] = temp;
            i = i - 1;
        }
        a[i + 1] = key;
    }

    cout << "elements after sorting using insertion sort are \n" << endl;
    for (i = 0; i < 6; i++) {
        cout << " " << a[i] << endl;
    }

    return 0;
}

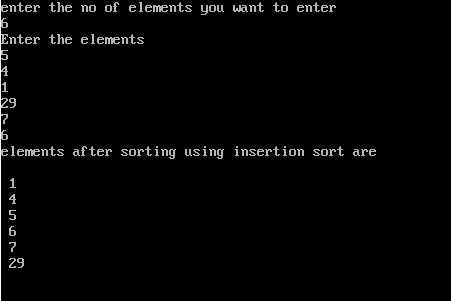
The output of the above program will be:

Insertion Sort Using Python

The below is the implementation of insertion sort using Python program:

import sys

def insertion_sort(arr):
    # This function will sort the array in non-decreasing order. 
    n = len(arr)
    # After each iteration first i+1 elements are in sorted order.
    for i in range(1, n):
        key = arr[i]
        j = i-1
        # In each iteration shift the elements of arr[0..i-1], 
        # that are greater than key, to one position ahead 
        # of their current position 
        while j >= 0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1 

        arr[j+1] = key
        
    return arr

# main code
if __name__=='__main__':

    arr = [24, 17, 66, 33, 72, 47, 68, 41, 105, 30]
    print("Sorted array: ")
    print(insertion_sort(arr))

The output of the above program will be:

Sorted array: 
[17, 24, 30, 33, 41, 47, 66, 68, 72, 105]