Home » Algorithms

Floyd Warshall algorithm with its Pseudo Code

In this article, we will learn about the concept of Floyd Warshall algorithm with its pseudo code.
Submitted by Shivangi Jain, on August 13, 2018

Floyd Warshall

The Floyd Warshall algorithm, itis the algorithm in which there is the use of different characterization of structure for a shortest path that we used in the matrix multiplication which is based on all pair algorithms. The algorithm considers the intermediate vertices of the shortest path, where an intermediate vertex of a simple path p =< v1, v2, ..., VL> is any vertex of p other than v1 or VL, that is, a vertex in the set {v2, v3,..., vl-1}.

The Floyd Warshall algorithm is based on the following observation. Suppose the vertices of the G be V = {1, 2,..., n}, and assume a subset {1, 2, ..., k} of the vertices for some k. For any pair of vertices i, j £ v consider that all paths from i to j which have their intermediate vertices all drawn from {1, 2,..., k}, and now let p be the minimum weight path from among them. The relationship between path p and shortest paths from i to j with all intermediate vertices in a set {1, 2,..., k-1} is exploited by the Floyd Warshall algorithm.

Let the weight of a shortest path from vertex i to the vertex j with all intermediate vertices in the set {1, 2, ..., k} be d (ij) ^ (k), when k = 0, a path from vertex i to vertex j with no intermediate vertex numbered higher than 0 has no intermediate vertices at all. It has at most one edge, hence (ij) ^ (0) = w (ij), A recursive definition is given by

d (ij) ^ (k) ={ w (ij)      if k = 0
{Min (d (ij) ^ (k-1), d (ik) ^ (k-1) + d (kj) ^ (k-1)   if k >= 1

Floyd Warshall Algorithm

    1.	n = rows [W]
    2.	D ^ (0) = W
    3.	For k = 1 to n
    4.	Do for I = 1 to n 
    5.	Do for j = 1 to n 
    6.	d (ij) ^ (k) = min (d(ij) ^ (k-1), d (ik) ^ (k-1) + d(kj) ^ (k-1))
    7.	return D ^ (n)

The running time of the Floyd Warshall algorithm is determined by the triply nested for loop of line 3 to 6. Each execution of the line 6 takes O (1) time. Thus the algorithm runs in O (n ^ 3) time.

In the Floyd Warshall algorithm, there are many ways for the constructing the shortest paths. One way is to compute the matrix D of the shortest path weights and then construct the predecessor matrix π from the matrix D. This method can be implemented to run in O (n ^ 3) time.

Example:

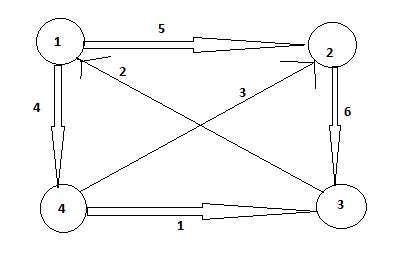
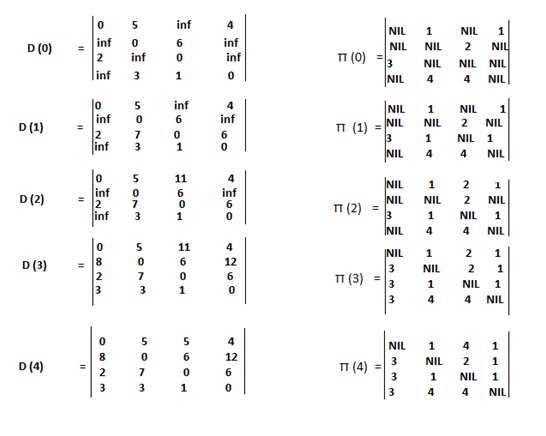
The sequence of matrices D ^ (k) and π ^ k (k computed by the Floyd Warshall algorithm) for given graph is computed as follows:

References: