Home »
Algorithms
Implement First Come First Served (FCFS) CPU Scheduling Algorithm using C program
First Come First Served (FCFS) CPU Scheduling Algorithm implementation: Here, we are going to implement FCFS scheduling algorithm using C program.
Submitted by Vipin Bailwal, on September 24, 2018
CPU scheduling decides which of the available processes in the ready queue is to be allocated the CPU. There are different CPU scheduling algorithms available. In this tutorial, we will learn about the First Come First Served Algorithm (FCFS) and see how we can implement it in C Programming Language?
First Come First Serve (FCFS)
First Come First Serve is the simplest and easiest scheduling algorithm. In this algorithm, the CPU is allocated to the processes in the order they request it. The implementation of FCFS is easily done with a queue (a FIFO structure). When the first process enters the system it starts its execution immediately and runs till it completes its execution. As other processes enter the system, they are put at the end of the queue and wait to get the CPU. When a process finishes executing, it releases the CPU, is removed from the queue and the CPU is allocated to next process at the head of the queue.
Example:
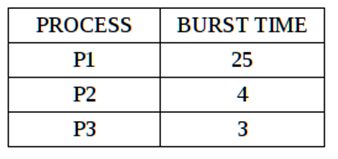
The processes arrive in the order P1, P2, P3 and are served as per the FCFS algorithm. The Gantt chart is as shown:

The waiting time for P1 is 0 milliseconds, for P2 it is 25 milliseconds and 29 milliseconds for P3. Thus, average waiting time is (0+25+29)/3 = 18 milliseconds.
Advantage:
- It is easy to understand and implement.
Disadvantage:
- It is a Non-Pre-emptive scheduling algorithm: Once a process has been allocated the CPU, it will not release the CPU until it finishes executing. Thus, it is not suitable for modern systems which work on the principle of time sharing.
- The Average Waiting Time is high.
- It results in CONVOY EFFECT i.e., many processes which require CPU for short duration have to wait for a bigger process to finish thus resulting in low resource utilization.
C program:
#include<stdio.h>
int main(){
int bt[10]={0},at[10]={0},tat[10]={0},wt[10]={0},ct[10]={0};
int n,sum=0;
float totalTAT=0,totalWT=0;
printf("Enter number of processes ");
scanf("%d",&n);
printf("Enter arrival time and burst time for each process\n\n");
for(int i=0;i<n;i++)
{
printf("Arrival time of process[%d] ",i+1);
scanf("%d",&at[i]);
printf("Burst time of process[%d] ",i+1);
scanf("%d",&bt[i]);
printf("\n");
}
//calculate completion time of processes
for(int j=0;j<n;j++)
{
sum+=bt[j];
ct[j]+=sum;
}
//calculate turnaround time and waiting times
for(int k=0;k<n;k++)
{
tat[k]=ct[k]-at[k];
totalTAT+=tat[k];
}
for(int k=0;k<n;k++)
{
wt[k]=tat[k]-bt[k];
totalWT+=wt[k];
}
printf("Solution: \n\n");
printf("P#\t AT\t BT\t CT\t TAT\t WT\t\n\n");
for(int i=0;i<n;i++)
{
printf("P%d\t %d\t %d\t %d\t %d\t %d\n",i+1,at[i],bt[i],ct[i],tat[i],wt[i]);
}
printf("\n\nAverage Turnaround Time = %f\n",totalTAT/n);
printf("Average WT = %f\n\n",totalWT/n);
return 0;
}
Output
Arrival time of process[3] 0
Burst time of process[3] 3
Solution:
P# AT BT CT TAT WT
P1 0 24 24 24 0
P2 0 3 27 27 24
P3 0 3 30 30 27
Average Turnaround Time = 27.000000
Average WT = 17.000000
Advertisement
Advertisement