Home » Algorithms

Midpoint Circle Algorithm

In this article, we are going to learn about circle generating algorithms in computer graphics i.e. Midpoint circle algorithm. Derivation of generating midpoint circle algorithm is also prescribed in this article.
Submitted by Abhishek Kataria, on August 04, 2018

Midpoint circle Algorithm

This is an algorithm which is used to calculate the entire perimeter points of a circle in a first octant so that the points of the other octant can be taken easily as they are mirror points; this is due to circle property as it is symmetric about its center.

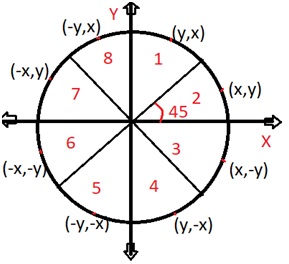
In this algorithm decision parameter is based on a circle equation. As we know that the equation of a circle is x² +y² =r² when the centre is (0, 0).

Now let us define the function of a circle i.e.: fcircle(x,y)= x² +y² - r²

1. If fcircle < 0 then x, y is inside the circle boundary.
2. If fcircle > 0 then x, y is outside the circle boundary.
3. If fcircle = 0 then x, y is on the circle boundary.

Decision parameter

p_k =fcircle(x_k+1,y_k-1/2) where p_k is a decision parameter and in this ½ is taken because it is a midpoint value through which it is easy to calculate value of y_k and y_k-1.

I.e. p_k= (x_k+1)²+ (y_k-1/2)²-r²

If p_k <0 then midpoint is inside the circle in this condition we select y is y_k otherwise we will select next y as y_k-1 for the condition of p_k > 0.

Conclusion

1. If p_k < 0 then y_k+1=y_k, by this the plotting points will be ( x_k+1 ,y_k). By this the value for the next point will be given as:
   P_k+1=p_k +2(x_k+1) +1
2. If p_k > 0 then y_k+1=y_k-1, by this the plotting points will be (x_k+1, y_k-1). By this the value of the next point will be given as:
   P_k+1=p_k+2(x_k+1) +1-2(y_k+1)

Initial decision parameter

P₀ = fcircle (1, r-1/2)

This is taken because of (x₀, y₀) = (0, r)

i.e. p₀ =5/4-r or 1-r, (1-r will be taken if r is integer)

ALGORITHM

1. In this the input radius r is there with a centre (x_c , y_c). To obtain the first point m the circumference of a circle is centered on the origin as (x₀,y₀) = (0,r).
2. Calculate the initial decision parameters which are:
   p₀ =5/4-r or 1-r
3. Now at each x_k position starting k=0, perform the following task.
   if p_k < 0 then plotting point will be ( x_k+1 ,y_k) and
   P_k+1=p_k +2(x_k+1) +1
   else the next point along the circle is (x_k+1, y_k-1) and
   P_k+1=p_k+2(x_k+1) +1-2(y_k+1)
4. Determine the symmetry points in the other quadrants.
5. Now move at each point by the given centre that is:
   x=x+x_c
   y=y+y_c
6. At last repeat steps from 3 to 5 until the condition x>=y.