Home » Algorithms

Multistage graph problem with forward approach and backward approach algorithms

In this article, we are going to learn about Multistage graph problem with its solution based on dynamic programming i.e. forward approach and backward approach algorithms for multistage graph.
Submitted by Shivangi Jain, on August 04, 2018

Multistage graph problem

1. The multistage graph problem is to find a minimum cost from a source to a sink.
2. A multistage graph is a directed graph having a number of multiple stages, where stages element should be connected consecutively.
3. In this multiple stage graph, there is a vertex whose in degree is 0 that is known as the source. And the vertex with only one out degree is 0 is known as the destination vertex.
4. The one end of the multiple stage graphs is at i thus the other reaching end is on i+1 stage.
5. If we denote a graph G = (V, E) in which the vertices are partitioned into K >= 2 disjoints sets, Vi, 1 <= I <=K. So that, if there is an edge < u, v > from u to v in E, the u £Vi and v € v (i+1), for some I, 1 <= i <= K. And sets V1 and Vk are such that |V1| = |Vk| = 1.

Algorithm for Forward Approach

    1.	F graph (graph G, int K, int n, int p[])
    2.	{
    3.	Float cost [max size], int d [max size], r;
    4.	Cost [n] = 0.0
    5.	For (int j = n-1; j>= 1; j--)
    6.	{
    7.	Let r be a vertex such that  is an edge of G and C[j][r] + cost[r] is minimum;
    8.	Cost [j] = C[j][r] + Cost[r]
    9.	D [j] = r
    10.	}
    11.	P [1] = 1 ,  P[k] = n
    12.	For (j = 2 ; j <= K-1; j++)
    13.	P[j] = d[P(j-1)];
    14.	}

Input = input is a K stage graph G = (V, E) with n vertices indexed in order of stages.

E is a set of an edge.

C [i][j] is the cost or weight of the edge [i][j]

Algorithm for Backward Approach

    1.	Algorithm BGraph (G, K, n, p)
    2.	// some function as FGraph
    3.	{
    4.	B cost [1] = 0.0;
    5.	For j = 2 to n do
    6.	{
    7.	// compute b cost [j].
    8.	Let r be such that  is an edge of 
    9.	G and b cost [r] + c [r, j];
    10.	D [j] = r;
    11.	}
    12.	// find a minimum cost path
    13.	P [1] = 1;              p [k] = n;
    14.	For j = k-1 to 2 do p[j] = d [p (j+1)];
    15.	}

If we consider s as the vertex in V1 and t as the vertex in Vk. The vertex s is supposed as the source and vertex t as the sink. The cost of a path from s to t is the sum of the costs of the edges on the path.

Here, each set Vi defines a stage in the graph. Each path starts from stage 1 goes to stage 2 then to stage 3 and so on, because of constraints on E.

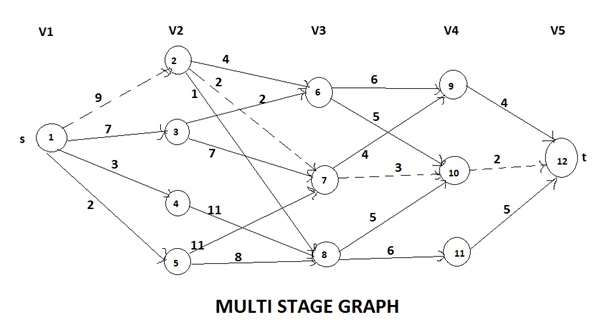
The minimum cost of s to t path is indicated by a dashed line. This method can be used for solving many problems such as allocating some resources to given number of projects with the intent to find the maximum profit.