Home »
Algorithms
P and NP problems and solutions | Algorithms
In this article, we learn about the concept of P problems, NP problems, NP hard problems and NP complete problems.
Submitted by Shivangi Jain, on July 29, 2018
P Problems
P is the set of all the decision problems solvable by deterministic algorithms in polynomial time.
NP Problems
NP is the set of all the decision problems that are solvable by non - deterministic algorithms in polynomial time.
Since deterministic algorithms are just the special case of non - deterministic ones, so we can conclude that P is the subset of NP.
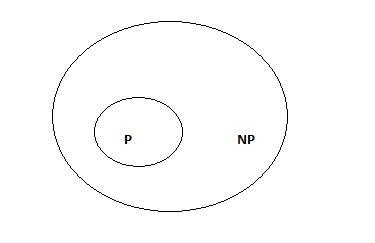
Relation between P and NP
NP Hard Problem
A problem L is the NP hard if and only if satisfiability reduces to L. A problem is NP complete if and only if L is the NP hard and L belongs to NP.
Only a decision problem can be NP complete. However, an optimization problem may be the NP hard. Furthermore if L1 is a decision problem and L2 an optimization problem, then it is possible that L1 α L2. One can trivially show that the knapsack decision problem reduces to knapsack optimization problem. For the clique problem one can easily show that the clique decision problem reduces to the clique optimization problem. In fact, one can also show that these optimization problems reduce to their corresponding decision problems.
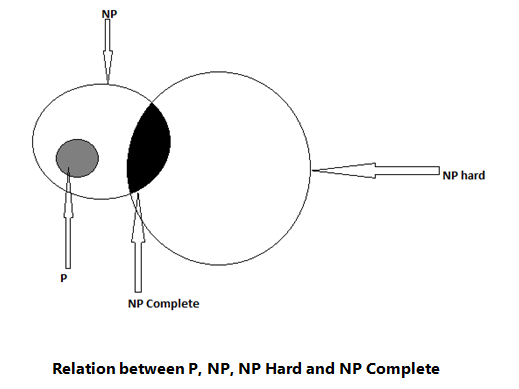
NP Completeness Problem
Polynomial time reductions provide a formal means for showing that one problem is at least as hard as another, within a polynomial time factor. This means, if L1 <= L2, then L1 is not more than a polynomial factor harder than L2. Which is why the “less than or equal to” notation for reduction is mnemonic. NP complete are the problems whose status are unknown.
Some of the examples of NP complete problems are:
1. Travelling Salesman Problem:
Given n cities, the distance between them and a number D, does exist a tor programme for a salesman to visit all the cities so that the total distance travelled is at most D.
2. Zero One Programming Problem:
Given m simultaneous equations,
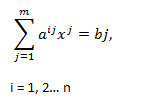
3. Satisfiability Problem:
Given a formula that involves propositional variables and logical connectives.
A language L is the subset [0, 1]* is NP complete if,
- L belongs to NP and
- L' ← L for every L' belongs to NP
All NP complete problems are NP hard, but some NP hard problems are not known to be NP complete.
If NP hard problems can be solved in polynomial time, then all the NP complete problems can be solved in polynomial time.
Advertisement
Advertisement