Home » Data Structure

Check if a given tree has all leaves at same level or not

In this article, we are going to check whether all leaves of the given tree is at the same level or not.
Submitted by Radib Kar, on August 07, 2020

The leave nodes are the nodes that don't have any children. Now a tree can have all leaves at the same level or not. We can check that using both recursive and iterative algorithms. Below is a detailed explanation of both the approaches & also we have added examples to understand how the algorithm is working.

Example 1:

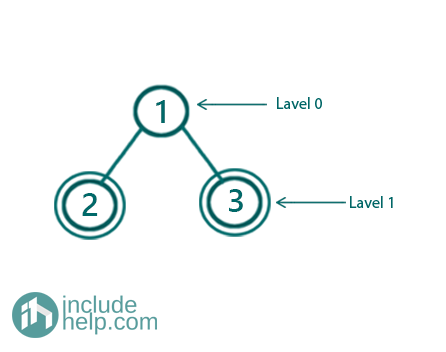
Figure 1: Example 1 where all leaf nodes are at the same level

In the above example, all the leaf nodes are marked with a double circle and we can see those are at the same level (Level 1).

Example 2:

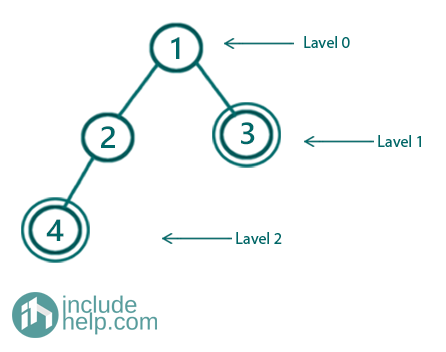
Figure 1: Example 1 where all leaf nodes are not at the same level

In the above example, all the leaf nodes are marked with a double circle and we can see all are not at the same level (one is at Level 1 and another is at level 2).

1) Recursive approach

In the recursive method, we can calculate the level of all leaf nodes and can store that in the hash table. Then in the second pass, we will check whether all leaf nodes have the same level or not from the hash table. So, after the first pass, we will have our hash table storing all leaf nodes along with their depth. The height() function in the below implementation is computing the levels of the leaf nodes recursively and storing them in the hashmap. Then in the second pass, we have checked whether all leaf nodes are at the same level or not. Below is the detailed implementation:

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void height(int level, TreeNode* root, unordered_map<TreeNode*, int>& mymap)
{
    //base case
    if (!root)
        return;

    //if current node is a leaf node
    //store it along with the current level in the hash table
    if (!root->left && !root->right) {
        mymap[root] = level;
        return;
    }

    //for the next level
    height(level + 1, root->left, mymap);
    height(level + 1, root->right, mymap);
}
bool checkAllLeavesAtSameLevel(TreeNode* root)
{
    //Your code here
    if (!root)
        return true;
    //first pass to store the leaf nodes along with their levels
    unordered_map<TreeNode*, int> mymap;
    height(0, root, mymap);

    //take height of any leaf node and make that bench mark
    int bench_mark = (mymap.begin())->second;
    //comapre other leaf node levels with the bench mark
    //if any leaf node violates, return false
    for (auto it = mymap.begin(); it != mymap.end(); it++) {
        if (it->second != bench_mark)
            return false;
    }
    //if all leaf nodes are at same level return true
    return true;
}

int main()
{
    //building the tree like example 1
    TreeNode* root1 = new TreeNode(1);
    
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);

    if (checkAllLeavesAtSameLevel(root1))
        cout << "Tree in example1 has all leaves at same level\n";
    else
        cout << "Tree in example1 doesn't has all leaves at same level\n";

    //building the tree-like example 2
    TreeNode* root2 = new TreeNode(1);
    root2->left = new TreeNode(2);
    root2->right = new TreeNode(3);
    root2->left->left = new TreeNode(4);

    if (checkAllLeavesAtSameLevel(root2))
        cout << "Tree in example2 has all leaves at same level\n";
    else
        cout << "Tree in example2 doesn't has all leaves at same level\n";
    
    return 0;
}

Output:

Tree in example1 has all leaves at same level
Tree in example2 doesn't has all leaves at same level

The time complexity of the above is O(n) and storage complexity is O(L) where L is the number of leaf nodes.

If we dry run, we will see that for the first example, after the first pass, we will have our hash table like below:

Key	                    Value
Tree Node with value 2	    1
Tree Node with value 3	    1

So all keys have the same value and hence the tree has all its leaves at the same level.

For the second example, after the first pass, we will have our hash table like below:

Key	                    Value
Tree Node with value 3	    1
Tree Node with value 4	    2

So we found that all keys don’t have the same value which means that all leaves are not at the same level.

2) Iterative approach(Using level order traversal)

We can also use iterative algorithms using level order traversal to solve this problem. The idea is to do a level order traversal and as soon as we find a leaf node, we set the benchmark to the current level where we find the leaf node. Then we keep traversing level wise and for each leaf node found, we check whether the current traversing level is the same as the benchmark level or not. Below is the detailed implementation.

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void height(int level, TreeNode* root, unordered_map<TreeNode*, int>& mymap)
{
    //base case
    if (!root)
        return;

    //if current node is a leaf node
    //store it along with the current level in the hash table
    if (!root->left && !root->right) {
        mymap[root] = level;
        return;
    }

    //for the next level
    height(level + 1, root->left, mymap);
    height(level + 1, root->right, mymap);
}

bool checkAllLeavesAtSameLevel(TreeNode* root)
{
    int bench_mark = INT_MIN;
    int cur_level = 0;
 
    queue<TreeNode*> q;
 
    q.push(root);
    q.push(NULL);
 
    //while queue is not empty
    while (!q.empty()) {
        TreeNode* cur_node = q.front();
        q.pop();
        //if DeQued element is NULL
        //that means end of last level
        if (!cur_node) {
            //increment the cure=rent level
            cur_level++;
            //if queue is not empty that means there are 
            //cuurent level nodes
            if (!q.empty()) {
                //add NULL to indicqate end of current level
                q.push(NULL);
            }
        }
        else {
            //if current node is leaf node
            if (!cur_node->left && !cur_node->right) {
                //if bench mark is not set yet
                if (bench_mark == INT_MIN) {
                    //first leaf node found
                    //set the bench mark as current level

                    bench_mark = cur_level;
                }
                else {
                    //for further leaf nodes check the bench mark same 
                    //with current level or not
                    if (cur_level != bench_mark)
                        return false;
                }
            }
            if (cur_node->left)
                q.push(cur_node->left);
            if (cur_node->right)
                q.push(cur_node->right);
        }
    }

    return true;
}

int main()
{
    //building the tree like example 1
    TreeNode* root1 = new TreeNode(1);
    
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);

    if (checkAllLeavesAtSameLevel(root1))
        cout << "Tree in example1 has all leaves at same level\n";
    else
        cout << "Tree in example1 doesn't has all leaves at same level\n";

    //building the tree-like example 2
    TreeNode* root2 = new TreeNode(1);
    
    root2->left = new TreeNode(2);
    root2->right = new TreeNode(3);
    root2->left->left = new TreeNode(4);

    if (checkAllLeavesAtSameLevel(root2))
        cout << "Tree in example2 has all leaves at same level\n";
    else
        cout << "Tree in example2 doesn't has all leaves at same level\n";
    
    return 0;
}

Output:

Tree in example1 has all leaves at same level
Tree in example2 doesn't has all leaves at same level