Home » Data Structure

Check if a subtree exists with the given sum

In this article, we are going to see how we can check whether a subtree exists with the given sum or not?
Submitted by Radib Kar, on September 15, 2020

In this article, we are going to see how we can check if there is any subtree exists with the given sum. For example,

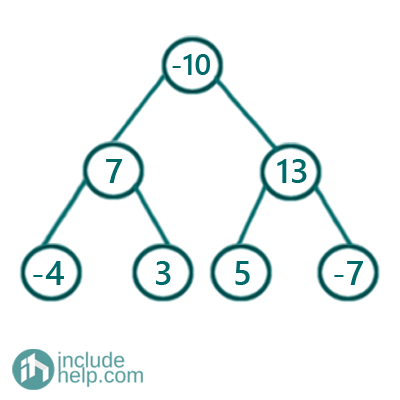
There is a subtree if the given sum is 6 and the subtree is,

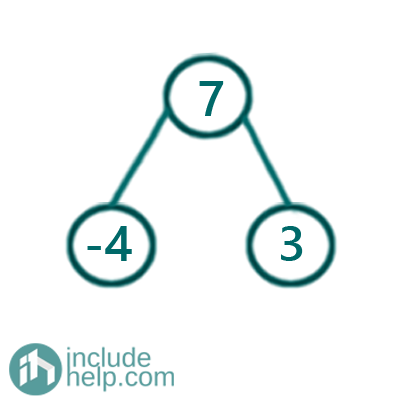
Of course, the brute force method is to find subtree sum rooted by each node and to check if the subtree sum matches with the input sum. But the complexity would be O(n^2).

So, the efficient approach is a recursive solution using postorder traversal which will solve in one pass. The algorithm is below:

Initially have a flag variable, answer set to FALSE which will change if we find any subtree with the given sum. And input sum is X.

FUNCTION maxSubtreeSumRecur(node, answer, X)    
    If node is NULL
        return 0;
    End IF
    if answer is TRUE
        then we already found the subtree so simply return any number 
    End IF  
    current sum= node value + left subtree sum(find recursively) + right subtree sum (find recursively) 
    if current sum ==X
        answer=TRUE
    return current sum which is the subtree sum rooted by node;
END FUNCTION

So, it's a postorder traversal which returns the subtree sum and we need to check if subtree sum is the same as the given sum.

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

int maxSubtreeSumRecur(TreeNode* node, int X, bool& answer)
{
    //if node is NULL return 0
    if (!node)
        return 0;
    //if answer is already true, then return anything, no need to proceed
    if (answer)
        return INT_MIN;

    int cur_sum = node->val + maxSubtreeSumRecur(node->left, X, answer) + maxSubtreeSumRecur(node->right, X, answer);
    
    if (cur_sum == X)
        answer = true;
    return cur_sum;
}

bool maxSubtreeSum(TreeNode* root, int X)
{
    bool answer = false;
    if (!root)
        return false;
    maxSubtreeSumRecur(root, X, answer);
    return answer;
}

int main()
{
    //building the tree like the example
    TreeNode* root = new TreeNode(-10);
    
    root->left = new TreeNode(7);
    root->right = new TreeNode(13);
    root->left->left = new TreeNode(-4);
    root->left->right = new TreeNode(3);
    root->right->left = new TreeNode(5);
    root->right->right = new TreeNode(-7);

    int X = 6;

    if (maxSubtreeSum(root, X))
        cout << "There is subtree found with given sum " << X << endl;
    else
        cout << "There is no subtree found with given sum " << X << endl;

    X = 12;
    if (maxSubtreeSum(root, X))
        cout << "There is subtree found with given sum " << X << endl;
    else
        cout << "There is no subtree found with given sum " << X << endl;

    return 0;
}

Output:

There is subtree found with given sum 6
There is no subtree found with given sum 12

Dry Run:

The tree is the given one same as example and the input sum is 6.

Since it's a postorder traversal we will show the dry run in bottom-up fashion as the recursion will reach their first before returning something.

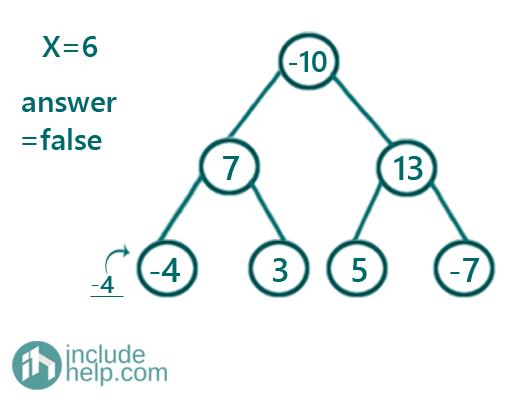
Figure 1: cur_sum is 4 which is not equal to given sum 6, so answer is false

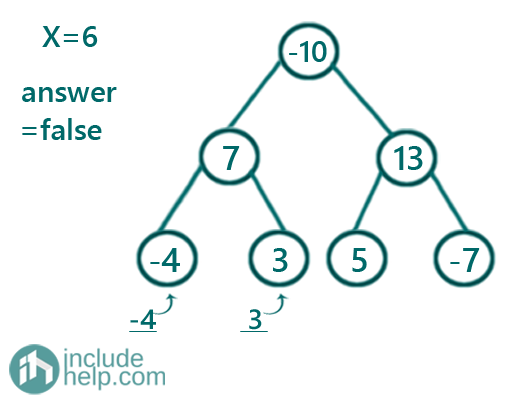
Figure 2: cur_sum is 3 which is not equal to given sum 6, so answer is false

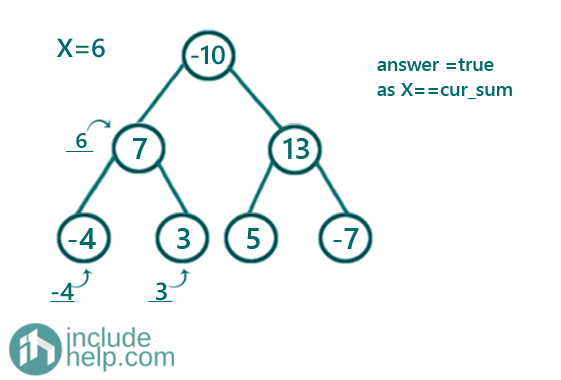
Figure 3: cur_sum is 6 which is not equal to given sum 6, so answer is true

Since the answer is true now in each further recursion it will simply return and reach the main calling function with answer = true. So, there is a subtree with the given sum 6.