Home » Data Structure

Check if the graph is tree or not

In this article, we are going to see how we can check whether the given graph is a tree or not?
Submitted by Radib Kar, on September 12, 2020

Prerequisite:

• N-array tree
• Cycle in Undirected graph | SET 1
• Cycle in Undirected graph | SET 2

In this article, we are going to see whether a graph is a tree or not. Before moving to the solution discussion, let us discuss when a graph can be a tree and what are the relation b/w tree and graph. First of all, here tree doesn't necessarily to be a binary Tree, rather when we discuss on tree v/s graph it's about a generic tree (N-array Tree).

In one word a generic tree is an acyclic undirected graph. So if an undirected graph doesn't have any cycle, then it can be treated as a tree (generic tree).

In the below example,

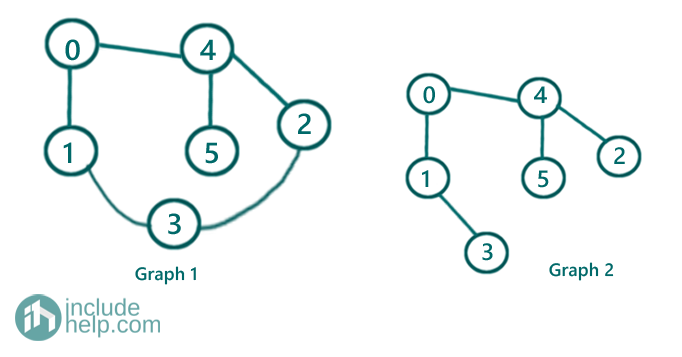
Graph1 is not a tree since it has a cycle, but the graph2 is a tree since it's acyclic. Moreover, it's a binary tree also which is not necessarily to be.

So to check whether a graph is tree or not we need to check whether the graph has a cycle or not. That we have already discussed in our previous articles. Please go through that for detailed discussion.   In the set1 we have used DFS and in the set2 we have used a more efficient approach based on disjoint set ADT operations.

Below is the code for disjoint set ADT implementation for cycle detection.

#include <bits/stdc++.h>
using namespace std;

int find(int x, vector<int>& parent)
{
    if (parent[x] == x)
        return x;
    return find(parent[x], parent);
}

void UNION(int x, int y, vector<int>& parent, vector<int>& rank)
{
    if (rank[x] > rank[y]) {
        parent[y] = x;
    }
    else if (rank[x] < rank[y]) {
        parent[x] = y;
    }
    else
        parent[y] = x;
}

bool isCyclic(vector<vector<int> >& edges, int V)
{
    vector<int> parent(V);
    
    for (int i = 0; i < V; i++)
        parent[i] = i;
    
    vector<int> rank(V, 0);

    for (auto edge : edges) {
        int x = find(edge[0], parent);
        int y = find(edge[1], parent);
        if (x != y)
            UNION(x, y, parent, rank);
        else
            return true;
    }
    return false;
}

int main()
{
    int n, m;

    cout << "Enter number of edges\n";
    cin >> n;
    cout << "Enter number of nodes\n";
    cin >> m;

    //edges list
    //each edge is a vector [u,v]
    vector<vector<int> > edges(n);

    for (int i = 0; i < n; i++) {
        int u, v;

        cout << "info for edge " << i + 1 << endl;
        cout << "Enter source node u: ";
        cin >> u;
        cout << "Enter destination node v: ";
        cin >> v;

        edges[i] = vector<int>{ u, v };
    }
    if (isCyclic(edges, m))
        cout << "The above undirected graph is not a tree\n";
    else
        cout << "The above undirected graph is a tree\n";

    return 0;
}

Output:

RUN 1:
Enter number of edges
6
Enter number of nodes
6
info for edge 1
Enter source node u: 0
Enter destination node v: 1
info for edge 2
Enter source node u: 0
Enter destination node v: 4
info for edge 3
Enter source node u: 1
Enter destination node v: 3
info for edge 4
Enter source node u: 4
Enter destination node v: 5
info for edge 5
Enter source node u: 4
Enter destination node v: 2
info for edge 6
Enter source node u: 2
Enter destination node v: 3
The above undirected graph is not a tree

RUN 2:
Enter number of edges
5
Enter number of nodes
6
info for edge 1
Enter source node u: 0
Enter destination node v: 1
info for edge 2
Enter source node u: 0
Enter destination node v: 4
info for edge 3
Enter source node u: 1
Enter destination node v: 3
info for edge 4
Enter source node u: 4
Enter destination node v: 5
info for edge 5
Enter source node u: 4
Enter destination node v: 2
The above undirected graph is a tree