Home » Data Structure

Check if two nodes are cousins in a binary tree

In this article, we are going to see how to check whether two nodes are cousin in the binary tree or not?
Submitted by Radib Kar, on August 05, 2020

Cousins in a Binary Tree

Two nodes are said to be cousins in a binary tree if they belong to the same level but their parent node is different. For example, in the below example,

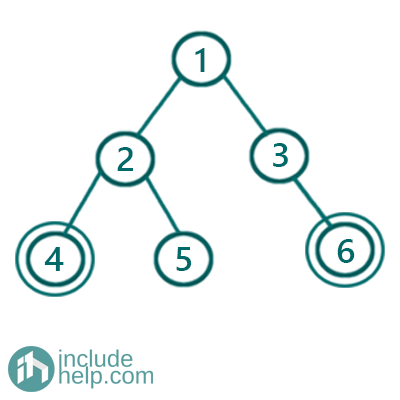
Figure 1: Example 1

Nodes with value 4 and 6 are cousin here as they are at the same level 2 and their parent is different. Node with value 4 has parent node with value 2 whereas node with value 6 has parent node with value 3. So they are cousins.

But in the below example,

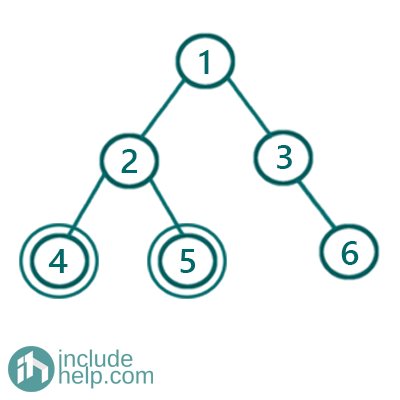
Node with value 4 and node with value 5 is not cousin, since they belong to the same parent.

Solution:

From the definition of a cousin in a tree, we can achieve the solution. The first thing is both the nodes need to be at the same level. So, here comes the level order traversal to determine the levels of the nodes to check. Secondly, we need to check whether the nodes have the same parent or not. For that, we need to store the parents of each node in the hash table for lookup.

So we can design an algorithm like below:

1)  Do a level order traversal
2)  If at any level a node(one out of those two nodes)   is found Then
        Look for the second Node
        If the second Node is found in this level, then
            Check their parents are the same or not
            If their parents are different, then they are cousins
            Else they are not cousin
        Else if the end of this level reaches without 
        finding the second node, then 
            They are not cousin  

Below is the detailed implementation of the same.

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

int sumTree(TreeNode* root)
{
    if (!root)
        return 0;

    //if current node is leaf node return it's sum
    if (!root->left && !root->right)
        return root->val;
    
    //left subtree sum
    int l = sumTree(root->left);
    
    //right subtree sum
    int r = sumTree(root->right);
    
    //if root val is equal to sum of left 
    //subtree + sum of right subtree then return the sum
    if (root->val == l + r)
        return root->val + l + r;
    else //otherwise return INT_MIN
        return INT_MIN;
}

bool isSumTree(TreeNode* root)
{
    if (!root)
        return true;
    //if function returns INT_MIN then it's not a sumTree
    if (sumTree(root) == INT_MIN)
        return false;
    return true;
}

int main()
{
    //building the tree like example 1
    TreeNode* root1 = new TreeNode(10);
    root1->left = new TreeNode(3);
    root1->right = new TreeNode(4);
    root1->left->left = new TreeNode(1);
    root1->left->right = new TreeNode(2);

    if (isSumTree(root1))
        cout << "Tree in example 1 is a Sum Tree\n";
    else
        cout << "Tree in example 1 is not a Sum Tree\n";

    //building the tree-like example 2
    TreeNode* root2 = new TreeNode(10);
    root2->left = new TreeNode(4);
    root2->right = new TreeNode(3);
    root2->left->left = new TreeNode(1);
    root2->left->right = new TreeNode(2);

    if (isSumTree(root2))
        cout << "Tree in example 2 is a Sum Tree\n";
    else
        cout << "Tree in example 2 is not a Sum Tree\n";
    
    return 0;
}

Output:

Tree in example 1 is a Sum Tree
Tree in example 2 is not a Sum Tree

If we dry run, for the first example, we will see that at level 2 we will find both. So it will enter the if(flag1 && flag2) statement and since parents of the nodes are different so, it will return true. Whereas, in the second example, since the parent of the nodes are same so it will return false.

There may be the case, where nodes are not at the same level, then, of course, it will return false by entering the if(flag1 || flag2) condition.