Home » Data Structure

Check if two trees are structurally similar or not

In this article, we are going to see how to check two trees are structurally similar or not?
Submitted by Radib Kar, on August 07, 2020

In this article, we going to see given two Tree roots how we can find whether two trees are structurally similar or not.

When we can say two trees are structurally similar?

For two trees are said to be structurally similar if the roots have the same structural subtrees. No matter what are the values of the roots, that doesn't have any impact on the structural similarity. Previously, we saw how to check if two trees are identical or not? The only difference in structural similarity is that we don't care about the root values. So, if we discard that root value checking, then we can use the same function identical() here too.

Say if structurally_similar() is a function that takes two tree nodes and returns true or false based on where they are structurally similar or not, then based on the above inference we can write like below

structurally_similar (root1, root2) returns  structurally_similar (root1->left,root2->left) && structurally_similar root1->right,root2->right))

That means it returns true only if both their left subtrees are structurally similar and both their right subtrees are structurally similar. Otherwise, it returns false.

To check whether both their left and right subtrees are equal or not we used the same function recursively.

Recursive function to check

Returns true if two trees are structurally same, otherwise false
bool structurally_identical(root1, root2){
    /////base cases/////    
    if (both roots are NULL)
        then they are structurally identical, so return true;
    if (one root is NULL & other is not)
        then they are not structurally identical, so return false;
    
    //no check for root values
    
    //recursively check both their subtrees
    return  structurally_identical (root1->left,root2->left) && 
            structurally_identical(root1->right,root2->right);
}

Example

1) When two trees are structurally identical

Below is the example where both the trees are structurally identical.

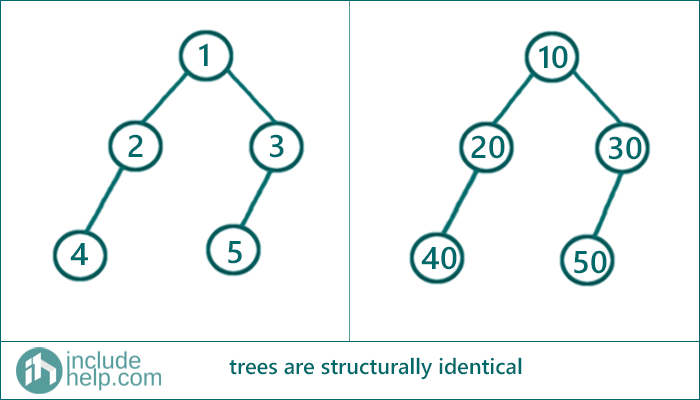
If we run a dry-run on the above tree. Then it starts with calling structurally_identical (1,10)

structurally_identical(1,10)
Since no root is NULL, it doesn't enter the base cases
//no checking for root value
So, it now checks for both subtree, 
call to structurally_identical (1->left, 10->left) && 
structurally_identical (1->right, 10->right)

structurally_identical (1->left, 10->left):
structurally_identical (2, 20)
Since no root is NULL, it doesn't enter the base case

//no checking for root value
So, it now checks for both subtree, 
call to structurally_identical (2->left, 20->left) && 
structurally_identical (2->right, 20->right)

structurally_identical (2->left, 20->left):
structurally_identical (4,40)
Since no root is NULL, it doesn't enter the base cases
//no checking for root value
So, it now checks for both subtree, 
call to structurally_identical (4->left, 40->left) && 
structurally_identical (4->right, 40->right)

Since, structurally_identical (4->left, 40->left) returns true 
as both roots are NULL. Same way, 
structurally_identical (4->right, 40->right) returns true

So, 
the entire function structurally_identical (2->left,20->left) returns true, 
that means the left subtree of root with value 2 & 
root with value 20 are structurally identical 

Similarly,
We can execute structurally_identical (2->right, 20->right) 
and that will return true also. 
So now structurally_identical (1->left, 10->left) returns true 
that means left subtree of our original roots are structurally identical.
We can find right subtrees are also structurally identical,

Hence both trees are structurally identical/similar.

2) When the two trees are not structurally identical

Below is the example where the trees are not structurally identical.

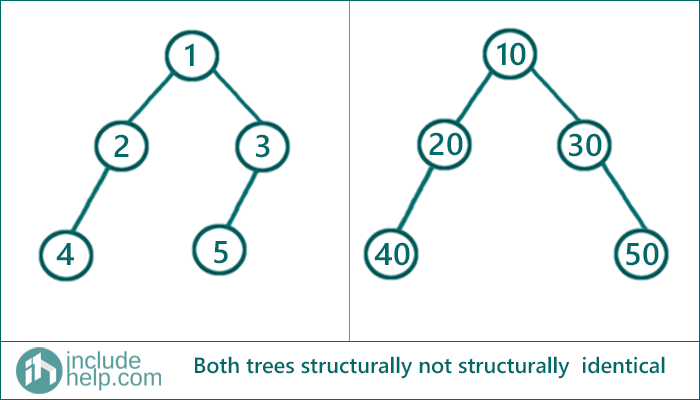
You can run a dry run of course, but since the length of the article will increase, I am skipping. But to point out why the above trees are not structurally identical and how our algorithm with detect

We can say that at the stage of calling structurally_identical(3,3) it will return false since the left child of 3 is 5 for the first tree whereas it's NULL for the second tree. So it will hit the second base case and return false. Once a function call returns false that will bubble up to the first function call and ultimately lead to an output false.

C Implementation:

#include <stdio.h>
#include <stdlib.h>

struct tree {
    int val;
    struct tree* left;
    struct tree* right;
};

typedef struct tree TreeNode;

TreeNode* newTree(int data)
{
    // Allocate memory for new node
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));

    // Assign data to this node val
    root->val = data;

    // Initialize left and right children as NULL
    root->left = NULL;
    root->right = NULL;
    return (root);
}

int structurally_identical(TreeNode* root1, TreeNode* root2)
{
    /////base cases/////
    //1.both roots are NULL then they are structurally identical
    if (root1 == NULL && root2 == NULL)
        return 1;
    //2.one root is NULL & other is not, 
    //then they are not structurally identical
    if (root1 == NULL || root2 == NULL)
        return 0;

    //no check for root values

    //recursively check both their subtrees
    return structurally_identical(root1->left, root2->left) && structurally_identical(root1->right, root2->right);
}

int main()
{
    //building the trees like example 1
    TreeNode* root1 = newTree(1);
    root1->left = newTree(2);
    root1->right = newTree(3);
    root1->left->left = newTree(4);
    root1->right->left = newTree(5);

    TreeNode* root2 = newTree(10);
    root2->left = newTree(20);
    root2->right = newTree(30);
    root2->left->left = newTree(40);
    root2->right->left = newTree(50);
    if (structurally_identical(root1, root2))
        printf("Both the trees in example1 are structurally identical\n");
    else
        printf("Both the trees in example1 are not structurally identical\n");

    //building the trees like example 2
    TreeNode* root3 = newTree(1);
    root3->left = newTree(2);
    root3->right = newTree(3);
    root3->left->left = newTree(4);
    root3->right->left = newTree(5);

    TreeNode* root4 = newTree(10);
    root4->left = newTree(20);
    root4->right = newTree(30);
    root4->left->left = newTree(40);
    root4->right->right = newTree(50);
    if (structurally_identical(root3, root4))
        printf("Both the trees in example2 are structurally identical\n");
    else
        printf("Both the trees in example2 are not structurally identical\n");
    
    return 0;
}

Output:

Both the trees in example1 are structurally identical
Both the trees in example2 are not structurally identical

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

bool structurally_identical(TreeNode* root1, TreeNode* root2)
{
    /////base cases/////
    //1.both roots are NULL then they are structurally identical
    if (root1 == NULL && root2 == NULL)
        return true;
    //2.one root is NULL & other is not, 
    //then they are not structurally identical
    if (root1 == NULL || root2 == NULL)
        return false;

    //no check for root values

    //recursively check both their subtrees
    return structurally_identical(root1->left, root2->left) && structurally_identical(root1->right, root2->right);
}

int main()
{
    //building the trees like example 1
    TreeNode* root1 = new TreeNode(1);
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);
    root1->left->left = new TreeNode(4);
    root1->right->left = new TreeNode(5);

    TreeNode* root2 = new TreeNode(10);
    root2->left = new TreeNode(20);
    root2->right = new TreeNode(30);
    root2->left->left = new TreeNode(40);
    root2->right->left = new TreeNode(50);
    if (structurally_identical(root1, root2))
        cout << "Both the trees in example1 are structurally identical\n";
    else
        cout << "Both the trees in example1 are not structurally identical\n";

    //building the trees like example 2
    TreeNode* root3 = new TreeNode(1);
    root3->left = new TreeNode(2);
    root3->right = new TreeNode(3);
    root3->left->left = new TreeNode(4);
    root3->right->left = new TreeNode(5);

    TreeNode* root4 = new TreeNode(10);
    root4->left = new TreeNode(20);
    root4->right = new TreeNode(30);
    root4->left->left = new TreeNode(40);
    root4->right->right = new TreeNode(50);
    if (structurally_identical(root3, root4))
        cout << "Both the trees in example2 are structurally identical\n";
    else
        cout << "Both the trees in example2 are not structurally identical\n";
    
    return 0;
}

Output:

Both the trees in example1 are structurally identical
Both the trees in example2 are not structurally identical