Home » Data Structure

Difference between Sum of Odd and Even Levels in a Given Binary Tree

In this article, we are going to see how to find difference between odd and even level sums by using level order traversal?
Submitted by Radib Kar, on September 01, 2020

Prerequisite: Level order traversal

Here, we are going to find how we can find the difference b/w odd & even level sums by using level order traversal. If you are not familiar with level order traversal then please have a look to the pre-requisite, please. Here, we need to identify which level is odd and which level is even. So we need two different accumulators which will accumulate even level sums and odd level sums respectively. If we identify a level as odd then we will add the current level sum to odd sum accumulator, otherwise, it will add to the even sum accumulator. Finally, we find the difference b/w odd and even level sum.

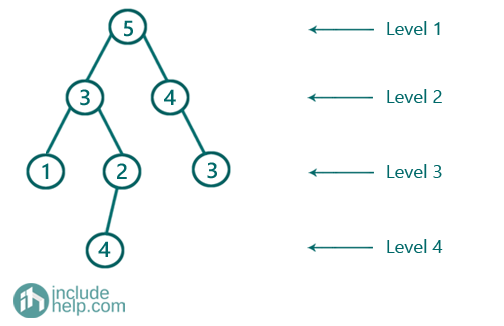
The level sums are:

Level 1->5 //odd level
Level 2-> 7 //even level
Level 3-> 6 //odd level
Level 4-> 4 //even level

Total even sum= 11
Total odd sum=11

So the difference is 0 here

The algorithm is:

1. oddsum is to store the odd level sums & evensum is to store the even level sums
2. Do a level order traversal & store current level sum to oddsum if the level is odd, otherwise, add the current level sum to evensum if the level is even.
3. To track the level is odd or not, we keep a flag variable, which keeps changing alternatively after completion of each level.

Below is the detailed implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

//Find the diff b/w odd even level sums
int oddEvenLevelSumDiff(TreeNode* root)
{
    queue<TreeNode*> q;
    
    int sum = 0;
    //to store sum for odd levels
    int oddsum = 0; 
    //to store sum for even levels
    int evensum = 0; 
    TreeNode* temp;

    //first level, root only
    q.push(root); 
    //end of first level
    q.push(NULL); 

    //odd is the flag, flag is true  as the 
    //starting level( level of root) is odd
    bool odd = true;
    //while queue is not empty
    while (!q.empty()) {
        //DeQueu
        temp = q.front();
        q.pop();
        //if end of current level
        if (temp == NULL) {
            //if queue is not empty place NULL at the end of 
            //the queue to denote end of upcoming level
            if (!q.empty()) {
                q.push(NULL);
            }

            if (odd) { //if it's odd level
                oddsum += sum; //add current level sum to odd level sum
                odd = false; //next level is even
            }
            else { //if it's even level
                evensum += sum;
                odd = true; //next level is odd
            }
            //since it's end of current level initialize sum as 
            //0 again to calculate for next level
            sum = 0;
        }
        else {
            sum += temp->val; //find current level sum
            //do level order traversal
            if (temp->left)
                q.push(temp->left);
            if (temp->right)
                q.push(temp->right);
        }
    }
    return abs(oddsum - evensum);
}

int main()
{
    //building the tree like the example
    TreeNode* root = new TreeNode(5);
    root->left = new TreeNode(3);
    root->right = new TreeNode(4);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(2);
    root->right->right = new TreeNode(3);
    root->left->right->left = new TreeNode(4);

    cout << "Difference b/w odd level sum & even level sum is: " << oddEvenLevelSumDiff(root) << endl;

    return 0;
}

Output:

Difference b/w odd level sum & even level sum is: 0

If we do the dry run for the above

The flag odd is set as true since the starting level( where the root is) is considered as odd

So, after completion of the first level, the current level sum is 5

And we add this to oddsum , so oddsum is now 5, and we change the flag to false now since next level is even.

So, after completion of the second level, the current level sum is 7

And we add this to evensum as the flag is set false, so evensum is now 5, and we change the flag to true now since next level is even.

So, on...

Finally, both the oddsum & evensum are 11 and thus the difference is 0.