Home » Data Structure

Lowest Common Ancestor in a Binary Tree | Set 1

In this article, we are going to see how to find the lowest common ancestor in a binary tree?
Submitted by Radib Kar, on August 08, 2020

Lowest common ancestor is the deepest ancestor of two given nodes. Below is the example, where we discuss what the Lowest Common ancestor of the given nodes is.

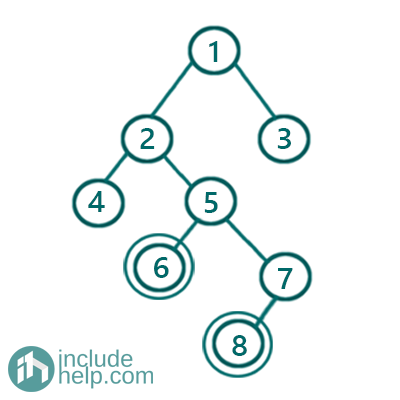
In the above tree, we are finding the lowest common ancestor for the nodes with value 6 & 8. To understand what lowest common ancestor is, first, we need to understand what is the ancestor for a node? Ancestor is the node that lies in the path b/w root and the current node. So the ancestors of the node 6 are 1, 2, 5 and the ancestors of the node 8 are 1, 2, 5, 7.

Common ancestors are the ancestors that are common in their list of ancestors. So the common ancestors are: 1, 2, 5

The lowest common ancestor means the ancestors that's the deepest one or in other words, the last ancestor in the common ancestor list. 

So, the lowest common ancestor is 5 here

So the algorithm to find the lowest common ancestor is like below:

1. Store the paths to the nodes from the roots
2. Find the common ancestors there. Common ancestors are the common nodes in the path starting from the root
3. The lowest common ancestor is the last common ancestor in the list.

Below is the implementation of the above approach:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

//calculates root to node paths
bool root_to_node_paths(TreeNode* root, TreeNode* node, vector<TreeNode*>& path)
{
    if (!root)
        return false;
 
    //if node is found
    if (root == node) {
        path.push_back(root);
        return true;
    }
 
    //add current node to path
    path.push_back(root);

    if (root_to_node_paths(root->left, node, path))
        return true;
    if (root_to_node_paths(root->right, node, path))
        return true;
    //backtrack
    path.pop_back();

    return false;
}

int main()
{
    //building the tree like example 1
    TreeNode* root = new TreeNode(1);
    
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->left->right->left = new TreeNode(6);
    root->left->right->right = new TreeNode(7);
    root->left->right->right->left = new TreeNode(8);

    TreeNode* node1 = root->left->right->left;
    TreeNode* node2 = root->left->right->right->left;

    vector<TreeNode*> path1;
    vector<TreeNode*> path2;
    
    //find root to node1 path
    root_to_node_paths(root, node1, path1);
    
    //find root to node2 path
    root_to_node_paths(root, node2, path2);

    int size = min(path1.size(), path2.size());

    TreeNode* LCA;
    
    //find all common ancestors
    cout << "Common ancestors are:\n";
    for (int i = 0; i < size; i++) {
        if (path1[i] == path2[i]) {
            LCA = path1[i];
            cout << path1[i]->val << " ";
        }
    }
    cout << endl;
    
    //LCA stores the last ancestor only which is the common one
    cout << "Lowest Common Ancestor is: " << LCA->val << endl;
    
    return 0;
}

Output:

Common ancestors are:
1 2 5 
Lowest Common Ancestor is: 5

So if we do the dry run then,

The root to node path for node1 will be, path1= 1, 2, 5, 6

The root to node path for node2 will be, path1= 1, 2, 5, 7, 8

So the common ancestors are: 1, 2, 5

And the lowest common ancestor is 5