Morris Traversal (Inorder) | Inorder traversal of binary Tree without recursion and without using Stack

Morris traversal is a traversal technique which uses the concept of threaded binary tree and helps to traversal any binary tree without recursion and without using stack (any additional storage). In this article we discuss Morris Traversal for inorder binary tree traversal.
Submitted by Radib Kar, on August 04, 2020

Prerequisite:

In this article, we are going to see, how we can traverse inorder without using recursion and any additional storage with the help of converting the tree to a threaded binary Tree?

In a threaded binary tree we link up the leaf nodes to point to its inorder successor. The same idea is bought into Morris Traversal. Below is the algorithm for Morris traversal and then we have presented a pictorial representation to describe the traversal step by step.

Algorithm:

1)  Set current_node as root 
2)  While current_node is not NULL
        If the current_node does not have any left child
            Print/traverse the current_node
            Move to the right child and update 
            current_node = current_node ->right
        Else
            Mark the current_node as right child of its 
            inorder predecessor & move to the left child, 
            i.e., 
            update current = current->left. But, if it's already 
            made as right child of its inorder predecessor 
            (that means done in any previous iterations) 
            then delete that link (It restores the tree back), 
            print/traverse the current node(because the left subtree is traversed) 
            and move to its right child, 
            i.e., 
            update current = current->right      		
    End While

What is inorder predecessor?

Inorder predecessor is the node that comes just before the current node in the inorder traversal. Normally for a node, the inorder predecessor is the rightmost node is its left subtree, like for the below example:

5 is inorder predecessor of the root 1 as that's the rightmost node in the left subtree as shown below,

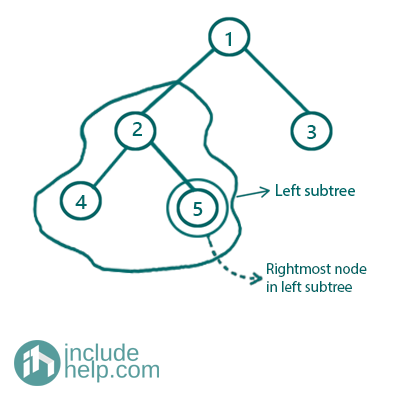
Figure 1: Inorder predecessor in a binary tree

Dry run with Example

The example tree is like below,

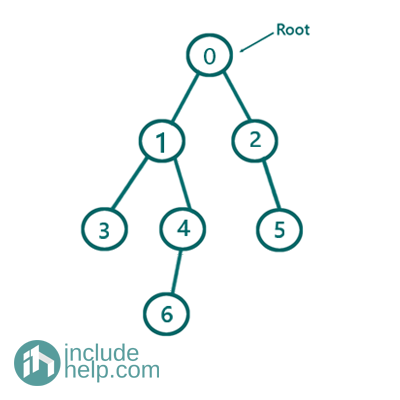
Figure 2: Original Binary Tree

Initially set current_node at root

Iteration 1:

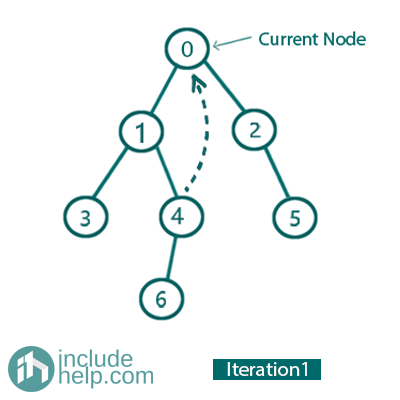
So, the current node is 0.

Left child is not NULL, mark 0 as right child of its inorder predecessor (node 4) so go to left and update current_node= current_node->left for the next iteration.

Iteration 2:

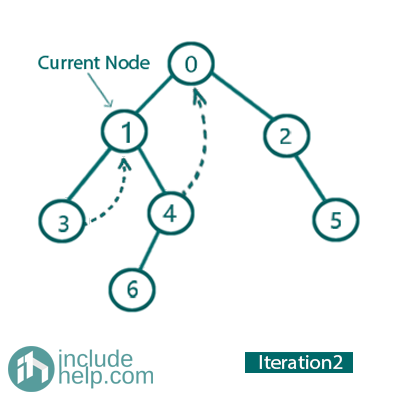
So, the current Node is 1 now.

Left child is not NULL, mark 1 as right child of its inorder predecessor (node 3) and go to left and update current_node= current_node->left for the next iteration.

Iteration 3:

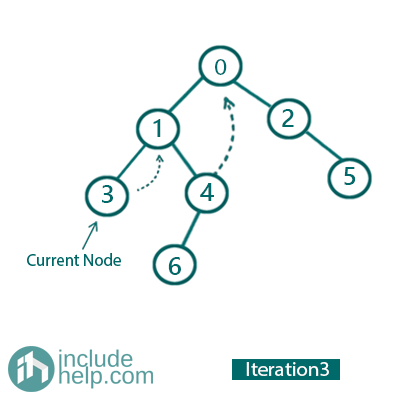
So, the current Node is 3

Left child is NULL

So, print/traverse the current node (It prints 3) and go to its right child. So, update current_node= current_node->right for the next iteration (see in the iteration 2 we set right child of 3 as 1).

Iteration 4:

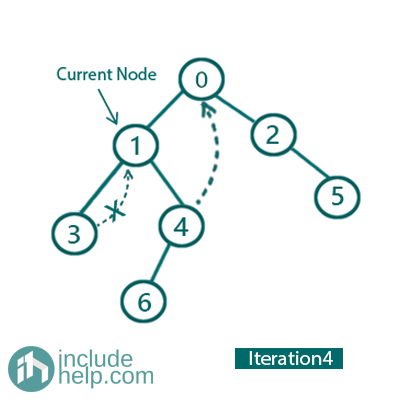
So, the current Node is 1.

Left child is not NULL, and 1 is already marked as right child of its inorder predecessor(node 3). So delete this link and print 1 & go to right and update current_node= current_node->right for the next iteration.

Iteration 5:

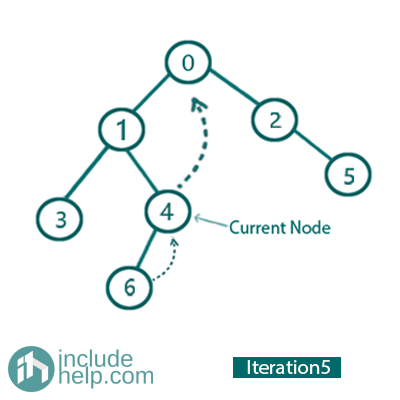
So, the current Node is 4.

Left child is not NULL, so mark 4 as right child of its inorder predecessor (node 6) and go to left and update current_node= current_node->left for the next iteration 6.

Iteration 6:

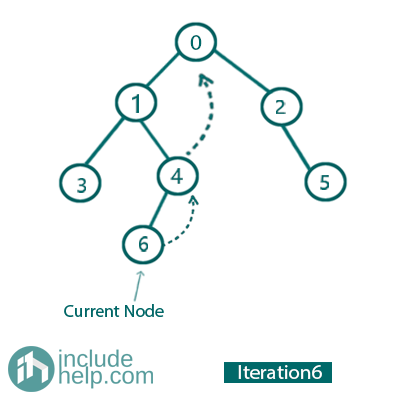
So, the current Node is 6.

Left child is NULL

So, print/traverse the current node (It prints 6) and go to its right child. So, update current_node= current_node->right for next iteration (see in the previous iteration we set right child of 6 as 4).

Iteration 7:

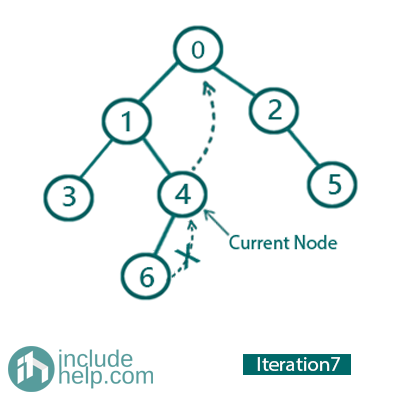
So, the current Node is 4.

Left child is not NULL, and 4 is already marked as right child of its inorder predecessor (node 6). So delete this link and print 4 and go to right and update current_node= current_node->right for next iteration (check its right child has been linked with 0 previously).

Iteration 8:

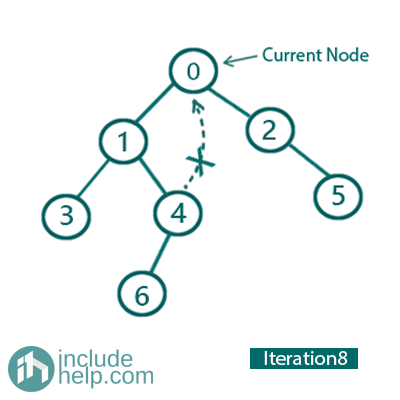
So, the current Node is 10.

Left child is not NULL, and 10 is already marked as right child of its inorder predecessor (node 4). So, delete this link and print 10 and go to right and update current_node= current_node->right.

Iteration 9:

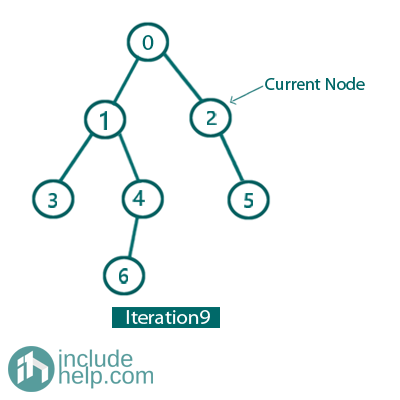
So, the current Node is 2.

Left child is NULL.

So, print/traverse the current node (It prints 2) and go to its right child. So, update current_node= current_node->right for next iteration no 10.

Iteration 10:

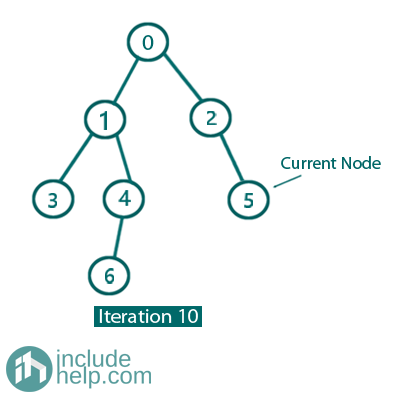
So, the current Node is 5.

Left child is NULL.

So, print/traverse the current node (It prints 5) and go to its right child. So, update current_node= current_node->right for next iteration.

Iteration 11:

Now the current node it NULL and thus it breaks the loop.

So, the overall traversal is:

3 1 6 4 0 2 5

3-> Got printed in iteration no 3
1-> Got printed in iteration no 4
6-> Got printed in iteration no 6
4-> Got printed in iteration no 7
0-> Got printed in iteration no 8
2-> Got printed in iteration no 9
5-> Got printed in iteration no 10

This is how Morris traversal works without recursion and without any extra storage. This has a time complexity of O(n) & a space complexity of O(1) , n be the number of nodes.

Below is the implementation for Morris inorder Traversal.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int v)
    {
        val = v;
        left = NULL;
        right = NULL;
    }
};

void inorderTraversal(TreeNode* root)
{
    TreeNode* current_node = root;
    
    while (current_node) {
        //if it has left child
        if (current_node->left) { 
            /*
            link current node as right child of the 
            rightmost node in left subtree (inorder predecessor)
            if not done already
            */
            //find rightmost node in left subtree
            TreeNode* rightmost_in_left_subtree = current_node->left;
            while (rightmost_in_left_subtree->right && rightmost_in_left_subtree->right != current_node) {
                rightmost_in_left_subtree = rightmost_in_left_subtree->right;
            }

            //if current node is not linked as right child to 
            //its inorder predecessor then link it
            if (!rightmost_in_left_subtree->right) {
                rightmost_in_left_subtree->right = current_node;
                //move to left now
                current_node = current_node->left;
            }

            else {
                /*
                if alreday found linked in,
                then it means it has already been 
                linked in any previous traversal 
                and we have finished traversing the left subtree
                so traverse the current node and remove 
                the link to restore tree
                */
                cout << current_node->val << " "; //print
                rightmost_in_left_subtree->right = NULL; //removed the link

                //move to right now since left subtree 
                //has been traversed already
                current_node = current_node->right;
            }
        }
        else {
            //traverse the node and move to right child
            cout << current_node->val << " ";
            current_node = current_node->right;
        }
    }
}

int main()
{
    //Tree is built like the example
    TreeNode* root = new TreeNode(0);
    
    root->left = new TreeNode(1);
    root->right = new TreeNode(2);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(4);
    root->right->right = new TreeNode(5);
    root->left->right->left = new TreeNode(6);
    
    cout << "Inorder traversal using Morris traversal is:\n";
    
    inorderTraversal(root);
    
    return 0;
}

Output:

Inorder traversal using Morris traversal is:
3 1 6 4 0 2 5

Comments and Discussions!

Load comments ↻