Home » Data Structure

Perfect Binary Tree

In this article, we are going to see what Perfect Binary Tree is and how to check whether a binary tree is perfect or not?
Submitted by Radib Kar, on August 03, 2020

Prerequisite: Binary Tree

What is a Perfect Binary Tree?

A Perfect Binary Tree is a special kind of binary tree where each and every internal node has exactly 2 children and all the leaf nodes lie at the same level.

For example, the below binary tree is a perfect binary tree whereas the second one is not.

Example 1:

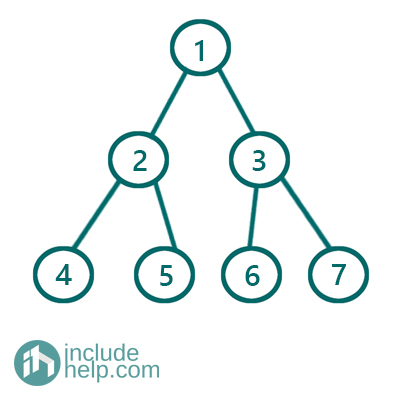
Figure 1: Perfect Binary Tree

The above example is a Perfect Binary Tree as every internal node in this has exactly two children and all the leaf nodes lie at the same level.

Example 2:

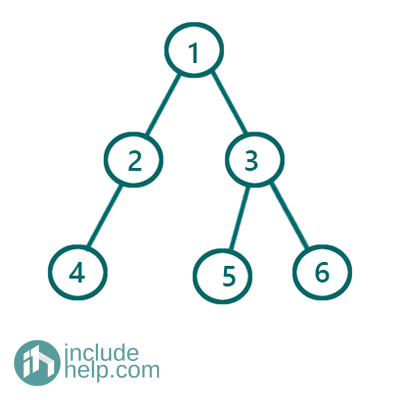
Figure 2: Binary Tree which is Not a Perfect Binary Tree

The above binary tree is not a perfect binary tree as all its internal nodes don't have exactly 2 children though all leaf nodes lie in the same level. The node having value 4 has only one child.

Properties for Perfect binary tree

There are few properties for Perfect binary tree which have been listed below:

Say,

Number of Total Nodes = N

Number of internal Nodes= I

Number of leaf Nodes= L

Height of the tree is: h

1. Number of total nodes in the perfect tree, N = 1+2+2²+…+2^h =2^{h + 1} – 1.
2. Number of leaf nodes in the perfect tree, L= 2^h
3. Height of the perfect binary tree is of range Θ(log₂(n)).

Check whether a Binary Tree is Perfect binary tree or not

To check whether a binary tree is perfect or not can be done by using perfect tree properties. As we saw that we can find a number of nodes if we know the height of the binary tree. So we simply count the nodes using recursion and check whether it follows the rule.

#include <bits/stdc++.h>
using namespace std;

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int v)
    {
        val = v;
        left = NULL;
        right = NULL;
    }
};

int height(TreeNode* root)
{
    if (!root)
        return 0;

    return 1 + max(height(root->left), height(root->right));
}

int count_no_of_nodes(TreeNode* root)
{
    if (!root)
        return 0;

    return 1 + count_no_of_nodes(root->left) + count_no_of_nodes(root->right);
}

//Perfect Binary Tree checking
bool is_Perfect_Binary_Tree(TreeNode* root)
{

    int h = height(root) - 1;
    int total_no_of_nodes = count_no_of_nodes(root);
    return pow(2, h + 1) - 1 == total_no_of_nodes;
}

int main()
{
    //Example 1 Tree is built
    TreeNode* root1 = new TreeNode(1);
    
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);
    root1->left->left = new TreeNode(4);
    root1->left->right = new TreeNode(5);
    root1->right->left = new TreeNode(6);
    root1->right->right = new TreeNode(7);

    if (is_Perfect_Binary_Tree(root1))
        cout << "The tree is Example 1 is a Perfect Binary Tree\n";
    else
        cout << "The tree is Example 1 is not a Prefect Binary Tree\n";

    //Example 2 Tree is built
    TreeNode* root2 = new TreeNode(1);
    root2->left = new TreeNode(2);
    root2->right = new TreeNode(3);
    root2->left->left = new TreeNode(4);
    root2->right->left = new TreeNode(5);
    root2->right->right = new TreeNode(6);

    if (is_Perfect_Binary_Tree(root2))
        cout << "The tree in Example 2 is a Perfect Binary Tree\n";
    else
        cout << "The tree in Example 2 is not a Perfect Binary Tree\n";

    return 0;
}

Output:

The tree is Example 1 is a Perfect Binary Tree
The tree in Example 2 is not a Perfect Binary Tree