Home » Data Structure

Preorder Traversal in Binary Tree Iteratively (without recursion)

In this article, we are going to find what preorder traversal of a Binary Tree is and how to implement preorder traversal iteratively without using recursion? We have provided the implementation in C++.
Submitted by Radib Kar, on July 30, 2020

In the earlier article on preorder traversal, we saw that preorder traversal is one of traversal which is based on depth-first search traversal. The basic concept for preorder traversal lies behind its name. "pre" means first/before and that's why the root is traversed before its left & right subtree. The basic rule is:

1. First, traverse the root
2. Then traverse the left subtree
3. Finally, traverse the right subtree

Of course, while traversing the subtrees we will follow the same order

We already saw a recursion based implementation. But here, we are going to discuss how to implement without recursion using stack iteratively.

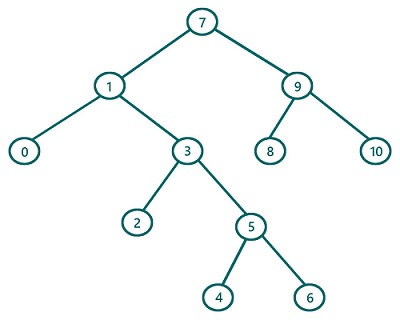
When we are using recursion, what we are doing is traversing the root first and then left subtree always and then t finally the right subtree. And we do this recursively for the subtrees. Like to traverse the right subtree, we again first traverse the root, then its left subtree and then again its right subtree if there any. Now to do this without recursion, we need stack which will do what recursion does. So the algorithm is:

1)  Define a stack st first & push root to stack.
2)  While (stack is not empty)
        Current=Pop stack and print //traversal of node 
        If(current->right is not NULL)
            Push current->right
        If(current->left is not NULL)
            Push current->left
    End While

In the above algorithm, we have put the right child first in the stack so that the left comes in the stack top and popped before the right child.

Dry Run using the above algorithm

Let's dry run the above example, using the above algorithm

We will use the value itself to represent the root

1) Define stack st & push the root(7) to stack
Stack now
7(top)

2) Processing the while loop:
--------------------------------------------------
Iteration 1
The stack is not empty, no enter the loop
Pop from the stack and thus current=7 and traverse/print this
So 7 got printed //prints 7
Current->right is not NULL
Thus push 7->right, 9 to stack
Current->left is not NULL
Thus push 7->left, 1 to stack

Now at this point, our stack is,
1 (top)
9
--------------------------------------------------
 
Iteration 2

The stack is not empty, no enter the loop
Pop from the stack and thus current=1 and traverse/print this
So 1 got printed //prints 1
Current->right is not NULL
Thus push 1->right, 3 to stack
Current->left is not NULL
Thus push 1->left, 0 to stack

Now at this point, our stack is,
0 (top)
3
9
--------------------------------------------------
Iteration 3

The stack is not empty, no enter the loop
Pop from the stack and thus current=0 and traverse/print this
So 0 got printed //prints 0
Current->right is NULL so no need to push
Current->left is NULL so no need to push

Now at this point, our stack is,
3(top)
9
--------------------------------------------------

Iteration 4
The stack is not empty, no enter the loop
Pop from the stack and thus current=3 and traverse/print this
So 3 got printed //prints 3
Current->right is not NULL
Thus push 3->right, 5 to stack
Current->left is not NULL
Thus push 3->left, 2 to stack

Now at this point, our stack is,
2 (top)
5
9

In this way, iterations will keep happening and it will 
stop only when the stack is empty which indicated end of traversal. 
I would suggest doing the dry run in paper and pen keeping 
the stack in front at every iteration.


Finally we will get traversal as:
7 1 0 3 2 5 4 6 9 8 10 

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode { 
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void preorder(TreeNode* root)
{
    //base case
    if (root == NULL)
        return;

    stack<TreeNode*> st;
    st.push(root);
    while (!st.empty()) {
        TreeNode* cur = st.top();
        st.pop();
        //traverse current node first
        cout << cur->val << " ";
        //put right subtree first
        if (cur->right)
            st.push(cur->right);
        //put left subtree then as it will 
        //stay in top for next iteration
        if (cur->left)
            st.push(cur->left);
    }
}

int main()
{
    //building the tree
    TreeNode* t = new TreeNode(7);
    
    t->left = new TreeNode(1);
    t->left->left = new TreeNode(0);
    t->left->right = new TreeNode(3);
    t->left->right->left = new TreeNode(2);
    t->left->right->right = new TreeNode(5);
    t->left->right->right->left = new TreeNode(4);
    t->left->right->right->right = new TreeNode(6);
    t->right = new TreeNode(9);
    t->right->left = new TreeNode(8);
    t->right->right = new TreeNode(10);

    printf("Preorder traversal of the above tree is:\n");
    preorder(t);
    
    return 0;
}

Output:

Preorder traversal of the above tree is:
7 1 0 3 2 5 4 6 9 8 10