Home » Data Structure

Reverse Inorder Traversal in Binary Tree (with recursion) in C, C++

In this article, we are going to find what is reverse inorder traversal of a Binary Tree and how to implement reverse inorder traversal using recursion? We have provided the implementation both in C & C++.
Submitted by Radib Kar, on July 24, 2020

Prerequisite: Inorder Traversal

If we classify tree traversals, inorder traversal is one of traversal which is based on depth-first search traversal.  Reverse inorder traversal is a modified version of inorder traversal sometimes needed for solving tree problems. The basic concept for reverse inorder traversal remains exactly same as of the inorder traversal, except the subtree traverse order. In normal inorder traversal we saw that

1. First, traverse the left subtree
2. Then traverse the root
3. Finally, traverse the right subtree

But in reverse inorder traversal instead of traversing the left subtree first, we traverse the right subtree first and then the left subtree. So the updated rules for reverse inorder traversal is:

1. First, traverse the right subtree
2. Then traverse the root
3. Finally, traverse the left subtree

Of course, while traversing the subtrees we will follow the same order

So let's traverse the below tree using reverse inorder traversal.

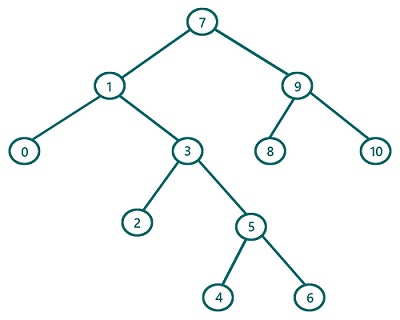
For the above tree, the root is: 7

Traverse the right subtree first(subtree rooted by 9)

Now to traverse the subtree rooted by 9, it again follows the same set of rules

So, traverse the right subtree of this (rooted by 10)

Since it's a leaf node we can print it as there is no more right subtree. Also, 10 has no left subtree, so this subtree rooted by 10 is traversed totally.

Traversal till now: 10

Since the right subtree of the subtree rooted 9 is traversed, now print the root 9 and traverse the left subtree (leaf node 8) in similar fashion. So, at this point,

Traversal till now: 10 9 8 and we are done with right subtree traversal of the original root 7. So, now traverse the root 7 and print that:

Traversal till now: 10 9 8 7

Now rest of the part is traversing the left subtree of the original root which is rooted by 1

After processing this subtree rooted by 1, we will have traversal: 10 9 8 7 6 5 4 3 2 1 0

The pseudocode would be:

void reverse_inorder(TreeNode root){
    if(root is NULL)
    return
    // recursively traverse right subtree first	
    reverse_inorder (right subtree of root) 
    // traverse current node
    print(root) 
    // recursively traverse left subtree first
    reverse_inorder (left subtree of root) 
}

C Implementation:

#include <stdio.h>
#include <stdlib.h>

struct tree {
    int val;
    struct tree* left;
    struct tree* right;
};

typedef struct tree TreeNode;

TreeNode* newTree(int data)
{
    // Allocate memory for new node
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));

    // Assign data to this node val
    root->val = data;

    // Initialize left and right children as NULL
    root->left = NULL;
    root->right = NULL;
    return (root);
}

void reverse_inorder(TreeNode* root)
{
    //base case
    if (root == NULL)
        return;

    //secondly traverse right sub tree
    reverse_inorder(root->right);

    //finally traverse current node
    printf("%d ", root->val);

    // fisrt traverse left sub tree
    reverse_inorder(root->left);
}

int main()
{
    //building the tree
    TreeNode* t = newTree(7);
    t->left = newTree(1);
    t->left->left = newTree(0);
    t->left->right = newTree(3);
    t->left->right->left = newTree(2);
    t->left->right->right = newTree(5);
    t->left->right->right->left = newTree(4);
    t->left->right->right->right = newTree(6);
    t->right = newTree(9);
    t->right->left = newTree(8);
    t->right->right = newTree(10);

    printf("Reverse inorder traversal of the above tree is:\n");
    reverse_inorder(t);

    return 0;
}

Output:

Reverse inorder traversal of the above tree is:
10 9 8 7 6 5 4 3 2 1 0

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

class TreeNode { // tree node is defined
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void reverse_inorder(TreeNode* root)
{
    //base case
    if (root == NULL)
        return;

    //secondly traverse right sub tree
    reverse_inorder(root->right);

    //finally traverse current node
    printf("%d ", root->val);

    // fisrt traverse left sub tree
    reverse_inorder(root->left);
}

int main()
{
    //building the tree
    TreeNode* t = new TreeNode(7);
    t->left = new TreeNode(1);
    t->left->left = new TreeNode(0);
    t->left->right = new TreeNode(3);
    t->left->right->left = new TreeNode(2);
    t->left->right->right = new TreeNode(5);
    t->left->right->right->left = new TreeNode(4);
    t->left->right->right->right = new TreeNode(6);
    t->right = new TreeNode(9);
    t->right->left = new TreeNode(8);
    t->right->right = new TreeNode(10);

    printf("Reverse Inorder traversal of the above tree is:\n");
    reverse_inorder(t);

    return 0;
}

Output:

Reverse Inorder traversal of the above tree is:
10 9 8 7 6 5 4 3 2 1 0