Home » Data Structure

Reverse Postorder Traversal in Binary Tree (using recursion) in C, C++

In this article, we are going to find what reverse postorder traversal of a Binary Tree is and how to implement reverse postorder traversal using recursion? We have provided the implementation both in C & C++.
Submitted by Radib Kar, on July 24, 2020

If we classify tree traversals, postorder traversal is one of the traversal techniques which is based on depth-first search traversal.  The basic concept for postorder traversal lies in its name itself. Post means "after" (last/finally) and that's why root is being traversed at last and its subtrees are being traversed first. Reverse postorder traversal is variation of postorder traversal where the subtree order is exact opposite than the normal postorder traversal. So, here the rule is:

1. First, traverse the right subtree
2. Then traverse the left subtree
3. Finally, traverse the root

Of course, while traversing the subtrees we will follow the same order

So let's traverse the below tree using preorder traversal.

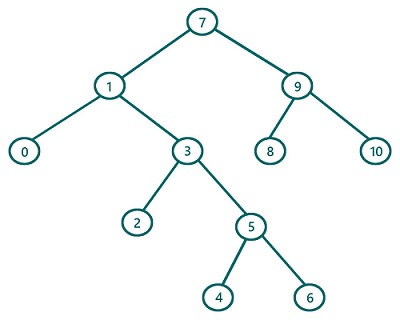
For the above tree, the root is: 7

So First Traverse the right subtree (Subtree rooted by 9)

Now to traverse the subtree rooted by 9, it again follows the same set of rules

So the First traverse its right subtree rooted by 10

Since it's a leaf node we can print it as there is no more right subtree. Also, 10 has no left subtree as well, so traverse 10 and this subtree rooted by 10(which is left subtree of 1) is traversed totally.

Traversal till now: 10

Now, traverse the left subtree of root 9(subtree rooted by 8). It again follows the same rule. After traversal of this subtree, we will have

Traversal till now: 10 8

Since we have traverse both the subtrees of subtree rooted by 9, now traverse the node 9 as per postorder traversal.

Now finally traverse root 9 is done we have completed both its subtrees and then the node itself

Traversal till now: 10 8 9

So right subtree is traversed for the original root 7

So, now traverse the left subtree of original root 7 which is rooted by 1 in the same way

After traversing the left subtree we will get: 10 8 9 6 4 5 2 3 0 1

Then finally traverse the root 7, so the final traversal will be: 10 8 9 6 4 5 2 3 0 1 7

The pseudocode would be:

void reverse_postorder(TreeNode root){
    if(root is NULL)
    return

    // recursively traverse right subtree
    reverse_postorder (right subtree of root) 
    //recursively traverse left subtree
    reverse_postorder (left subtree of root) 
    print(root) //traverse current node	
}

C Implementation:

Tree structure:

struct tree{
  int val;
  struct tree* left;
  struct tree* right;
};
typedef struct tree TreeNode;

#include <stdio.h>
#include <stdlib.h>

struct tree {
    int val;
    struct tree* left;
    struct tree* right;
};

typedef struct tree TreeNode;

TreeNode* newTree(int data)
{
    // Allocate memory for new node
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));

    // Assign data to this node val
    root->val = data;

    // Initialize left and right children as NULL
    root->left = NULL;
    root->right = NULL;
    return (root);
}

void reverse_postorder(TreeNode* root)
{
    //base case
    if (root == NULL)
        return;

    //First traverse right sub tree
    reverse_postorder(root->right);
    // Secondly traverse left sub tree
    reverse_postorder(root->left);

    //finally traverse current node
    printf("%d ", root->val);
}

int main()
{
    //building the tree
    TreeNode* t = newTree(7);
    
    t->left = newTree(1);
    t->left->left = newTree(0);
    t->left->right = newTree(3);
    t->left->right->left = newTree(2);
    t->left->right->right = newTree(5);
    t->left->right->right->left = newTree(4);
    t->left->right->right->right = newTree(6);
    t->right = newTree(9);
    t->right->left = newTree(8);
    t->right->right = newTree(10);

    printf("Reverse postorder traversal of the above tree is:\n");
    reverse_postorder(t);
    
    return 0;
}

Output:

Reverse postorder traversal of the above tree is:
10 8 9 6 4 5 2 3 0 1 7 

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

class TreeNode { // tree node is defined
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void reverse_postorder(TreeNode* root)
{
    //base case
    if (root == NULL)
        return;

    //First traverse right sub tree
    reverse_postorder(root->right);
    // Secondly traverse left sub tree
    reverse_postorder(root->left);

    //finally traverse current node
    printf("%d ", root->val);
}

int main()
{
    //building the tree
    TreeNode* t = new TreeNode(7);
    
    t->left = new TreeNode(1);
    t->left->left = new TreeNode(0);
    t->left->right = new TreeNode(3);
    t->left->right->left = new TreeNode(2);
    t->left->right->right = new TreeNode(5);
    t->left->right->right->left = new TreeNode(4);
    t->left->right->right->right = new TreeNode(6);
    t->right = new TreeNode(9);
    t->right->left = new TreeNode(8);
    t->right->right = new TreeNode(10);
    
    printf("Reverse Postorder traversal of the above tree is:\n");
    reverse_postorder(t);
    
    return 0;
}

Output:

Reverse Postorder traversal of the above tree is:
10 8 9 6 4 5 2 3 0 1 7