Home » Data Structure

Find height of a binary tree using recursive approach | Set 1

In this article, we are going to see how to find height of a binary tree recursively? Height of a Binary tree is basically the path length from root to the deepest leaf node. Here, we have discussed the approach and provided implementation both in C & C++.
Submitted by Radib Kar, on July 30, 2020

What is height of a binary tree?

The height of a binary tree can be defined in many ways. We are giving two most relevant definitions which can help to solve the problem, i.e. to find the height of a binary tree.

1. Height of a binary tree can be thought of the longest path length from root to the deepest leaf.
2. In other word height of a binary tree can be defined as 1+ maximum (height of left subtree, height of right subtree) which is of course a recursive definition.

Both of the above definition helps to find the height of the binary tree, but in this tutorial we will focus only on the second definition which helps to find the height recursively. We have also discussed the first definition is another tutorial here (Find Height of a Binary Tree using level order tree traversal | set 2

So,

Height (original tree) = 1+ maximum(Height(left subtree)+ Height(right subtree)) where Height is the recursive function and takes input a Tree root.

The details of the above recursive function can be written as:

Function height( TreeNode root) returns int which is the height
    int height(TreeNode root):
        //base case
        if root is NULL
            return 0
        //1 is for the height of root
        return 1+ maximum (height(root->left, height(root->right))

Let check how the above algorithm is working on the below example:

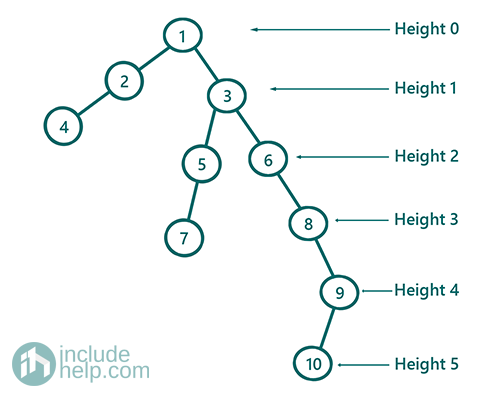
Do define a node we will use its value.

So in the main function, we call height(1) //1 is root

Function height(1):
Root(1) is not NULL
So call 1+ max(height(1->left) +height(1->right))
So it calls height(1->left) first

Function height(2):
Root(1) is not NULL
So call 1+ max(height(2->left) +height(2->right))
So it calls height(2->left) first

Function height(4):
Root(4) is not NULL
So call 1+ max(height(4->left) +height(4->right))
So it calls height(4->left) first

Function height(NULL):
Root(NULL) is  NULL so return 0
Return goes back to Function height(4)
Now it calls height(4->height)

Function height(NULL):
Root(NULL) is  NULL so return 0
So return again goes back to Function height(4)
It returns 1+max(0,0)=1 back to function  height(2)
So now it calls height(2->right) 

Function height(NULL):
Root(NULL) is NULL so return 0

So now, Function height(2) return 1+max(1,0)=2 
to function height(1->left)

Now in Function height(1) we have the height of 
its left subtree and that's 2

Now it will calls height(1->right) to find its right subtree height 
which we can find similar way and the value would be 5
So height of the tree is
1+max(2,5)=6

That's how recursion solves the problem and below is the C & C++ implementations.

C Implementation:

#include <stdio.h>
#include <stdlib.h>

struct tree {
    int val;
    struct tree* left;
    struct tree* right;
};

typedef struct tree TreeNode;

TreeNode* newTree(int data)
{
    // Allocate memory for new node
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));

    // Assign data to this node val
    root->val = data;

    // Initialize left and right children as NULL
    root->left = NULL;
    root->right = NULL;
    return (root);
}

int max(int a, int b)
{

    return (a >= b) ? a : b;
}

//to find the height
int height(TreeNode* root)
{
    //base case
    if (root == NULL)
        return 0;

    //tree height = 1+maximum 
    //(left subtree height,right subtree height)
    return 1 + max(height(root->left), height(root->right));
}

int main()
{
    //building the tree
    TreeNode* t = newTree(1);
    
    t->left = newTree(2);
    t->left->left = newTree(4);
    t->right = newTree(3);
    t->right->left = newTree(5);
    t->right->right = newTree(6);
    t->right->left->left = newTree(7);
    t->right->right->right = newTree(8);
    t->right->right->right->right = newTree(9);
    t->right->right->right->right->left = newTree(10);

    printf("Height of the tree is: %d", height(t));

    return 0;
}

Output:

Height of the tree is: 6

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

int height(TreeNode* root)
{
    //base case
    if (root == NULL)
        return 0;

    //tree height = 1+maximum
    //(left subtree height,right subtree height)
    return 1 + max(height(root->left), height(root->right));
}

int main()
{
    //building the tree
    TreeNode* t = new TreeNode(1);
    
    t->left = new TreeNode(2);
    t->left->left = new TreeNode(4);
    t->right = new TreeNode(3);
    t->right->left = new TreeNode(5);
    t->right->right = new TreeNode(6);
    t->right->left->left = new TreeNode(7);
    t->right->right->right = new TreeNode(8);
    t->right->right->right->right = new TreeNode(9);
    t->right->right->right->right->left = new TreeNode(10);
    
    cout << "height of the tree is :" << height(t);

    return 0;
}

Output:

height of the tree is :6