Home » Data Structure

Find Height of a Binary Tree using level order tree traversal | set 2

In this article we are going to see how to find height of a binary Tree using level order tree traversal? We have implemented the above in C++.
Submitted by Radib Kar, on July 30, 2020

Prerequisite: Height of binary tree using recursion, Level order

In the pre-requisite article, we saw what we define as the height of the binary tree and we found two most relevant definitions. Out of one which is recursive definition already implemented in set 1.

The second one was about finding the deepest node and the height will be the length of the path from the root to the deepest node (There can be many deepest nodes, but we need to take care of anyone).

The idea is to do a level order traversal keeping track of start and end of each level. Each level corresponds to each height/depth of the tree. For example, in the below tree,

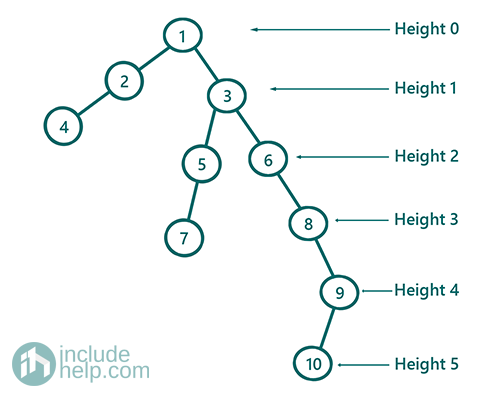
There are 6 levels namely,
Level0-> 1
Level1-> 2, 3
Level2-> 4, 5, 6
Level3-> 7, 8
Level4-> 9
Level5-> 10

So what we have to do is too distinguish b/w two consecutive levels and we will increment a counter at start of each level. To distinguish b/w levels or to indicate end of a level, we inject a dummy NULL Node like below algorithm.

1)  Initialize a queue q
2)  Push root node to the queue and then push NULL to indicate end of level0
3)  Set counter 0
4)  while(queue, q is not empty){
        temp=DeQueue(q);  //Dequeue
        if(temp==NULL){
            indicates end of the last level reached
            So increment counter
            //that means there are still some 
            //nodes of next level
            If(queue is not empty()) 
                EnQueue(NULL)		
    }
    Else{
        if(temp->left)
            EnQueue(q,temp->left); // if left child exists EnQueue
        if(temp->right)
            EnQueue(q,temp->right); // if right child exists EnQueue
    }
    End While
5) counter will give the result which is the height of the tree

Dry run of the above example,

Initially queue is empty and counter=0
So push root and then NULL to the tree
So queue now
1(root) (front)
NULL(rear)

Iteration1:
Queue front is 1 and so temp will be 1 after the DeQueue step
Temp is not NULL
Thus it enters the else condition
EnQueue 1->left
EnQueue 1->right
Queue now:
NULL(front)
2(1->left)
3(1->right)(rear)

Iteration2:
Queue front is NULL and so temp will be NULL after the DeQueue step
Temp is NULL
So, it determines end of the last level 
((see the last level was level 0 with element 1 that got traversed))
So increment counter and thus counter is now 1
Since, queue is not empty so we will EnQueue NULL 
to indicate end of current level
Queue now:
2(1->left) (front)
3(1->right)
NULL(rear)

Iteration3:
Queue front is 2 and so temp will be 2 after the DeQueue step
Temp is not NULL
Thus it enters the else condition
EnQueue 2->left
2->right is NULL, so it won’t be EnQueued
Queue now:
3(1->right)(front)
NULL
4(2->left) (rear)

Iteration4:
Queue front is 3 and so temp will be 3 after the DeQueue step
Temp is not NULL
Thus it enters the else condition
EnQueue 3->left
EnQueue 3->right
Queue now:
NULL(front)
4(2->left) 
5(3-left)
6(3->right) (rear)

Iteration5:
Queue front is NULL and so temp will be NULL after the DeQueue step
Temp is NULL
Increment the counter as it means end of prev level 
(see the last level was level 1 with elements 2 & 3 that got traversed)
Since queue is not empty EnQueue NULL to indicate end of current level
Counter is now 2
Queue now:
4(2->left) (front) 
5(3-left)
6(3->right) (rear)

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

int height(TreeNode* root)
{
    queue<TreeNode*> q;
    TreeNode* temp;
    q.push(root);
    q.push(NULL);
    int counter = 0;
    while (!q.empty()) {
        temp = q.front();
        q.pop();
        if (temp == NULL) { //end of last level

            counter++; //increment height
            if (!q.empty())
                q.push(NULL); //end of current level
        }
        else {
            if (temp->left)
                q.push(temp->left); //EnQueue
            if (temp->right)
                q.push(temp->right); //EnQueue
        }
    }
    return counter;
}

int main()
{
    //building the tree
    TreeNode* t = new TreeNode(1);

    t->left = new TreeNode(2);
    t->left->left = new TreeNode(4);
    t->right = new TreeNode(3);
    t->right->left = new TreeNode(5);
    t->right->right = new TreeNode(6);
    t->right->left->left = new TreeNode(7);
    t->right->right->right = new TreeNode(8);
    t->right->right->right->right = new TreeNode(9);
    t->right->right->right->right->left = new TreeNode(10);

    cout << "height of the tree is :" << height(t);

    return 0;
}

Output:

height of the tree is :6