Home » Data Structure

Print all cousins of a node in the given tree

In this article, we are going to see how to print all cousins of a node in a given binary tree?
Submitted by Radib Kar, on August 21, 2020

Prerequisite: Check if two nodes are cousin

In the last article, we saw what we mean by cousin nodes. Two nodes are said to be cousins in a binary tree if they belong to the same level but their parent node is different. Now the thing is a node can have many cousins and here we will see how to find all the cousins.

For example, in the below tree,

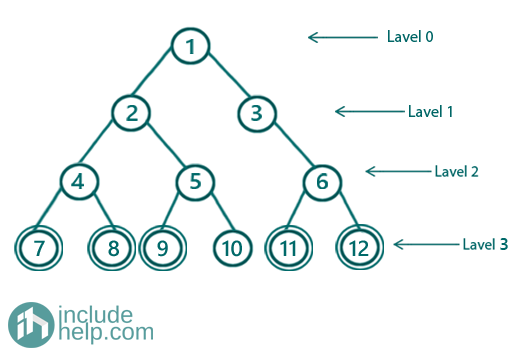
Cousins for a node with value 9 is all the nodes at the same level except the one which has the same parent( If the node is the only child then there won’t be any such)

So, the algorithm is:

1. Collect nodes level wise and keep storing parent for every node in a hash table.
2. If the node is found at the current level, then print all nodes in this level(stored) whose parent is not the same as the found node’s parent.
3. If the node is not found at the current level, then delete stored nodes of the current level

If we do a dry run of the algorithm,

Then after processing the 0^th level, we have stored 1, but node 9 is not found, so delete the stored node(s).

Then after processing the 1^st level, we have stored {2, 3}, but node 9 is not found, so delete the stored nodes.

Then after processing the 2^nd level, we have stored {4, 5, 6}, but node 9 is not found, so delete the stored nodes

Then after processing the 3^rd level, we have stored {7, 8, 9, 10, 11, 12}, and node 9 is found, so print all nodes, whose parents are different. Node with value 10 has the same parent as of node 9, so we will print other nodes. Hence, the output would be: 7, 8, 11, 12 (Of course, we will not print 9!)

Below is the implementation:

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int data)
    {
        val = data;
        left = NULL;
        right = NULL;
    }
};

void Print_All_Cousins(TreeNode* root, int x)
{
    if (!root) {
        cout << "Empty Tree\n";
        return;
    }

    queue<TreeNode*> q;
    map<TreeNode*, TreeNode*> parents;

    q.push(root);
    q.push(NULL);
    int level = 0;
    TreeNode* store;
    //initially none of the nodse found
    bool flag = false;
    vector<TreeNode*> sameLevelNodes;

    //do level order traversal
    while (!q.empty()) {
        TreeNode* temp = q.front();
        q.pop();
        if (!temp) {
            //end of current level
            if (!q.empty()) {
                q.push(NULL);
            }
            //if node is found at the current level, end processing
            //sameLevelNodes has all nodes in 
            //this level where the given node is
            if (flag) {
                break;
            }
            else //othrwise we have no use of the current level
                sameLevelNodes.clear();
        }
        else {
            //node with value x
            sameLevelNodes.push_back(temp);
            if (temp->val == x) {
                flag = true;
                //store the found node
                store = temp;
            }

            if (temp->left) {
                //store parent
                parents[temp->left] = temp;
                q.push(temp->left);
            }
            if (temp->right) {
                //store parent
                parents[temp->right] = temp;
                q.push(temp->right);
            }
        }
    }
    if (sameLevelNodes.size() == 0) {
        cout << "Given node doesn't exist\n";
    }
    else {
        for (auto it : sameLevelNodes) {
            if (it != store && parents[it] != parents[store])
                cout << it->val << " ";
        }
        cout << endl;
    }
}

int main()
{
    //building the tree like example
    TreeNode* root = new TreeNode(1);

    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->right = new TreeNode(6);
    root->left->left->left = new TreeNode(7);
    root->left->left->right = new TreeNode(8);
    root->left->right->left = new TreeNode(9);
    root->left->right->right = new TreeNode(10);
    root->right->right->left = new TreeNode(11);
    root->right->right->right = new TreeNode(12);

    //example1
    Print_All_Cousins(root, 9);

    //Example 2

    Print_All_Cousins(root, 15);
    return 0;
}

Output:

7 8 11 12 
Given node doesn't exist