Home » Interview coding problems/challenges

Check a graph is Hamiltonian or not (Hamiltonian path)

Hamiltonian path: In this article, we are going to learn how to check is a graph Hamiltonian or not?
Submitted by Souvik Saha, on May 11, 2019

Problem statement

Given a graph G. you have to find out that that graph is Hamiltonian or not.

Example:

Input:

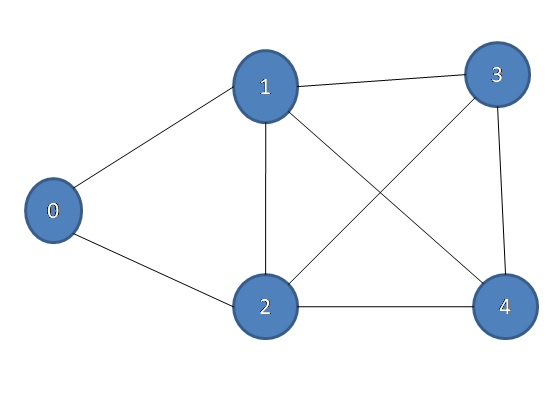
Output: 1

Because here is a path 0 → 1 → 5 → 3 → 2 → 0 and 0 → 2 → 3 → 5 → 1 → 0

Algorithm:

To solve this problem we follow this approach:

1. We take the source vertex and go for its adjacent not visited vertices.
2. Whenever we find a new vertex we make it source vertex and we repeat step 1.
3. When a vertex count is equal to the vertex number then we check that from vertex is there any path to the source vertex. If there is exist a path to the source vertex then we will mark it and if not then make that vertex as unmarked and continue the process.
4. If there is no such path then we say NO.

C++ Implementation to check a graph is Hamiltonian or not

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

void addedge(list<int>* g, int u, int v)
{
    g[u].push_back(v);
    g[v].push_back(u);
}

int hamiltonian(list<int>* g, int v, int s, int& count, bool* vis, int& h)
{
    if (count > 1 && s == 0) {
        h = 1;
        return 1;
    }
    list<int>::iterator it;
    for (it = g[s].begin(); it != g[s].end(); it++) {
        if (!vis[*it]) {
            vis[*it] = true;
            count++;
            if (count == v) {
                vis[0] = false;
            }
            hamiltonian(g, v, *it, count, vis, h);
            vis[0] = true;
            vis[*it] = false;
            count--;
        }
    }
    return 0;
}

int main()
{
    int num;
    cin >> num;
    for (int i = 0; i < num; i++) {
        int v, e;
        cin >> v >> e;
        list<int> g[v];
        int x, y;
        for (int j = 0; j < e; j++) {
            cin >> x >> y;
            addedge(g, x, y);
        }
        bool vis[v];
        memset(vis, false, sizeof(vis));
        int count = 1;
        vis[0] = true;
        int h = 0;
        hamiltonian(g, v, 0, count, vis, h);
        cout << h << endl;
    }
    return 0;
}

Output

1
5
8
0 1
0 2
1 2
1 3
1 4
3 4
3 2
2 4
1