Home » Interview coding problems/challenges

Two Mirror Trees

In this article, we are going to see how to find whether a tree is mirror reflection of another tree or not? This problem has been featured in the coding round of D.E.Shaw, Hike and Amazon. Submitted by Radib Kar, on December 22, 2018

Problem statement: Given a Two Binary Trees, write a function that returns true if one is mirror of other, else returns false.

Solution

Check the below examples:

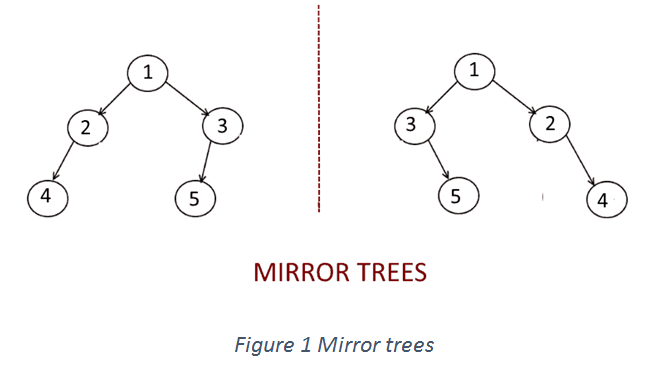
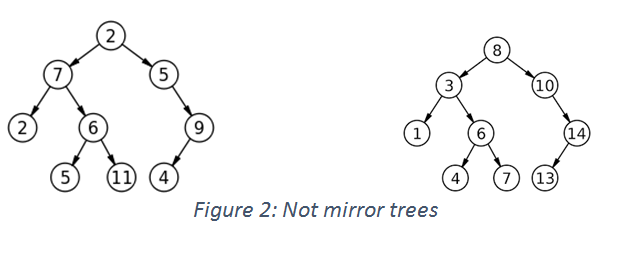
In figure 1, both the trees have the same root and one tree is mirror of other. Where as in In Figure 2, both trees are identical in shape and thus are not mirror trees at all and have different node values too.

So in general, two trees are said to be mirror trees of each other if they have the same root , left subtree (from root) of first tree is mirror of right subtree of second tree & right subtree of the first tree is mirror of left subtree of second tree.

These are the three necessary & sufficient conditions to be checked for finding mirror trees.

Algorithm

1.  Define tree structure like:
    class tree{    // tree node is defined
        public:
        int data;
        tree *left;
        tree *right;
    };

    Or you can use struct instead of class
2.  Build both of the input tree.
3.  Recursive function AreMirror to check whether 
    both trees are mirror tree or not.

FUNCTION AreMirror (root of first tree, root of second tree)
    Root of first tree, root1
    Root of second tree root2
    FUNCTION AreMirror (root1, root2) 
        a.  Check base cases
            If root1==NULL&&root2==NULL
            Then it's mirror tree, return true;
            If root1==NULL || root2==NULL
            Then it's not a mirror tree, return false
            Because one root is NULL whether another is not. 
            (Both can't be NULL here, since already checked before) 
            If root1->data != root2->data
            Then it's not a mirror tree, return false.
            Because roots are different & thus can't be mirror image of other
        b.  Recursively check for sub-trees
            return(AreMirror(root1->left, root2->right) 
            &&AreMirror(root1->right,root2->left));
END FUNCTION

Explanation with example

Let's check how the program works for the first example...

N.B: Nodes are represented by their respective values.

Root1=1 and Root2=1
In the main it calls AreMirror (1, 1)
--------------------------------------------------

AreMirror (1, 1):
1->left =2 and 1->right=3 in case of tree1
1->left =3 and 1->right=2 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror ( 2, 2) && AreMirror ( 3, 3))
Call to AreMirror ( 2, 2) and AreMirror ( 3, 3)
--------------------------------------------------

AreMirror (2, 2):(call at AreMirror (1, 1))
2->left =4 and 2->right=NULL in case of tree1
2->left =NULL and 2->right=4 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (4, 4) && AreMirror (NULL, NULL))
Call to AreMirror (4, 4) and AreMirror (NULL, NULL))
--------------------------------------------------

AreMirror (3, 3): (call at AreMirror (1, 1))
3->left =5 and 3->right=NULL in case of tree1
3->left =NULL and 3->right=5 in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (5, 5) && AreMirror (NULL, NULL))
Call to AreMirror (5, 5) && AreMirror (NULL, NULL)
--------------------------------------------------

AreMirror (4, 4): (call at AreMirror (2, 2))
4->left =NULL and 4->right=NULL in case of tree1
4->left =NULL and 4->right=NULL in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (NULL, NULL) && AreMirror (NULL, NULL))
Call to AreMirror (NULL, NULL) && AreMirror (NULL, NULL)
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (2, 2))
Base case matches and returns 1. 
--------------------------------------------------

AreMirror (5, 5): (call at AreMirror (3, 3))
5->left =NULL and 5->right=NULL in case of tree1
5->left =NULL and 5->right=NULL in case of tree2
No base cases are satisfied thus it returns,
(AreMirror (NULL, NULL) && AreMirror (NULL, NULL))
Call to AreMirror (NULL, NULL) && AreMirror (NULL, NULL)
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (3, 3))
Base case matches and returns 1. 
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (4, 4))
Base case matches and returns 1. 
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (4, 4))
Base case matches and returns 1. 
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (5, 5))
Base case matches and returns 1. 
--------------------------------------------------

AreMirror (NULL, NULL): (call at AreMirror (5, 5))
Base case matches and returns 1. 
--------------------------------------------------

Thus at main,
AreMirror (1, 1) returns:
=   AreMirror ( 2, 2) && AreMirror ( 3, 3)
=   (AreMirror (4, 4) && AreMirror (NULL, NULL)) && 
    (AreMirror (5, 5) && AreMirror (NULL, NULL))
=   ((AreMirror (NULL, NULL) && AreMirror (NULL, NULL)) && 1) 
    &&((AreMirror (NULL, NULL) && AreMirror (NULL, NULL)) && 1)
=   ((1 && 1) &&1) && (1 && 1) &&1)
=   1

Thus they are mirror trees

C++ implementation to check whether two trees are mirros?

#include<bits/stdc++.h>
using namespace std;

class tree{    // tree node is defined
	public:
	int data;
	tree *left;
	tree *right;
};
tree* newnode(int data)  // creating new node
{ 
    tree* node = (tree*)malloc(sizeof(tree)); 
    node->data = data; 
    node->left = NULL; 
    node->right = NULL; 
  
    return(node); 
} 


//function to check mirror tree
int areMirror(tree* a, tree* b)
{
   // base cases
   //if both root is NULL, then it's mirror tree
   if(a==NULL && b==NULL)
   return 1;
   //if one is NULL & other is not
   //then it's not mirror tree
   if(a==NULL || b==NULL)
   return 0;
   //if root data are different
   //not mirror tree
   if(a->data!=b->data)
   return 0;
   //check for subtrees recursively 
   return(areMirror(a->left,b->right) && areMirror(a->right,b->left));
   
}


int main(){
    //**same tree is builted as shown in example 1**
	cout<<"**same trees are built as shown in example 1**\n";
	tree *root1=newnode(1); 
    root1->left= newnode(2); 
    root1->right= newnode(3); 
    root1->left->left=newnode(4);
    root1->right->left=newnode(5);
    
	
    tree *root2=newnode(1); 
    root2->left= newnode(3); 
    root2->right= newnode(2); 
    root2->right->right=newnode(4);
    root2->left->right=newnode(5); 
    
    cout<<"printing whether mirror trees...\n"; 
    if(areMirror(root1,root2))//if returns 1
    cout<<"Both are mirror of each other\n";
    else
    cout<<"not mirror of each other\n";
    
    
    
    //**same tree is builted as shown in example 2**
	cout<<"**same trees are built as shown in example 2**\n";
	
    root1=newnode(2); 
    root1->left= newnode(7); 
    root1->right= newnode(5); 
    root1->right->right=newnode(9);
    root1->right->right->left=newnode(4);
    root1->left->left=newnode(2); 
    root1->left->right=newnode(6);
    root1->left->right->left=newnode(5);
    root1->left->right->right=newnode(11);
  
    root2=newnode(8); 
    root2->left= newnode(3); 
    root2->right= newnode(10); 
    root2->right->right=newnode(14);
    root2->right->right->left=newnode(13);
    root2->left->left=newnode(1); 
    root2->left->right=newnode(6);
    root2->left->right->left=newnode(4);
    root2->left->right->right=newnode(7);
      
    
    cout<<"printing whether mirror trees...\n"; 
    if(areMirror(root1,root2))//if returns 1
    cout<<"Both are mirror of each other\n";
    else
    cout<<"not mirror of each other\n";
        
    return 0;
       
 }

Output

**same trees are built as shown in example 1**
printing whether mirror trees...
Both are mirror of each other
**same trees are built as shown in example 2**
printing whether mirror trees...
not mirror of each other