Home » Interview coding problems/challenges

Tug of War

Tug of War: Here, we are going to learn to the solution of a problem to divide a set of number to two different set where both the subset contains same number of element and have a minimum difference of sum between them using backtracking. Submitted by Souvik Saha, on February 03, 2020

Description

This is a standard interview problem to divide a set of number to two different set where both the subset contains same number of element and have a minimum difference of sum between them using backtracking.

Problem statement

There is a set contains N number of elements. We have to divide this set into two different sets where each of the subsets contains the same number of elements and has a minimum difference between them.

1. If N is even then each of the subsets will contain N/2 number of elements.
2. If N is odd then one of the subsets will contain (N+1)/2 and others will contain (N-1)/2 number of elements.

    Input:
    Test case T
    //T no. of line with the value of N and corresponding values.
    E.g.
    3
    3
    1 2 3
    4
    1 2 3 4
    10
    1 4 8 6 -7 -10 87 54 16 100
    1<=T<=100
    1<=N<=100

    Output:
    Print the two subsets.

Examples

    T=3
    N=3
    1 2 3

    Output:  set1: {1, 2} set2: {3}

    N=4
    1 2 3 4

    Output: set1: {1, 4} set2: {2, 3}

    N=10
    1 4 8 6 -7 -10 87 54 16 100
    Output: set1: {{ 4, -7, -10, 87, 54 } set2: {1, 8, 6, 16, 100 }

Explanation with example

Let, there is N no. of values, say e₁, e₂, e₃, ..., e_n and N is even.

    Subset1: { N/2  no. of values }
    Subset2: { N/2 no. of values }

The process to insert the elements to the Subsets is a problem of combination and permutation. To get the result we use the backtracking process. Here we take the sum of all the elements 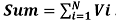. Here we have to find out the elements that are in the subset no.1 and the elements that are not in subset1, must be in the subset no. 2. Every time we consider two things.

1. The i^th element is a part of the subset1.
2. The i^th element is not a part of the subset1.

After getting N/2 number of elements into the subset1. We will check,

If the value is less than then Difference we update the value of the Difference and make a note of the elements that are in the subset1.

After getting the elements for those the value of Difference is less we check the elements of the main set and find out the elements that are not in the subset1 and put them in subset2.

    Set: {1, 2, 3}
    Sum=6

1. 1 is in the subset1 therefore Subset1: {1} and Difference = abs(3-1) = 2
2. 2 is in the subset1 therefore Subset1: {1,2} and Difference = abs(3-3) = 0

Therefore, Difference is minimum.

    Subset1: {1,2}
    Subset2: {3}

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

void traverse(int* arr, int i, int n, int no_of_selected, int sum, int& diff, bool* take, vector<int>& result, vector<int> current, int current_sum)
{
    //if the current position is greater than or equals to n
    if (i >= n)
        return;

    //if the value of difference is greater than
    //Sum/2-current sum of the elements of Subset no.1
    if ((diff > abs(sum / 2 - current_sum)) && (no_of_selected == (n + 1) / 2 || no_of_selected == (n - 1) / 2)) {
        diff = abs(sum / 2 - current_sum);
        //store the subset no. 1
        result = current;
    }

    //taking the elemets after the current element one by one
    for (int j = i; j < n; j++) {
        take[j] = true;
        current.push_back(arr[j]);
        traverse(arr, j + 1, n, no_of_selected + 1, sum, diff, take, result, current, current_sum + arr[j]);
        current.pop_back();
        take[j] = false;
    }
}

void find(int* arr, int n)
{
    //array to distinguished the elements those are in subset no. 1
    bool take[n];
    int sum = 0;

    for (int i = 0; i < n; i++) {
        sum += arr[i];
        take[i] = false;
    }

    int diff = INT_MAX;
    int no_of_selected = 0;

    vector<int> result;
    vector<int> current;

    int current_sum = 0;
    int i = 0;

    traverse(arr, i, n, no_of_selected, sum, diff, take, result, current, current_sum);

    set<int> s;

    //elements those are in subset no.1
    cout << "Set1 : { ";
    for (int j = 0; j < result.size(); j++) {
        cout << result[j] << " ";
        s.insert(result[j]);
    }
    cout << "}" << endl;

    //elements those are in subset no.2
    cout << "Set2 : { ";
    for (int j = 0; j < n; j++) {
        if (s.find(arr[j]) == s.end()) {
            cout << arr[j] << " ";
        }
    }
    cout << "}" << endl;
}

int main()
{
    int t;

    cout << "Test case : ";
    cin >> t;

    while (t--) {
        int n;
        cout << "Enter the value of n : ";
        cin >> n;
        int arr[n];
        cout << "Enter the values: ";
        //taking the set elements
        for (int i = 0; i < n; i++) {
            cin >> arr[i];
        }
        find(arr, n);
    }
    return 0;
}

Output

Test cases : 3
Enter the value of n : 3
Enter the values: 1 2 3
Set1 : { 1 2 }
Set2 : { 3 }
Enter the value of n : 4
Enter the values: 1 2 3 4
Set1 : { 2 3 }
Set2 : { 1 4 }
Enter the value of n : 10
Enter the values: 1 4 8 6 -7 -10 87 54 16 100
Set1 : { 4 -7 -10 87 54 }
Set2 : { 1 8 6 16 100 }