Home » Interview coding problems/challenges

Longest Common Subsequence of three strings

Longest Common Subsequence of three strings: This is an extension of the normal longest common subsequence program for two strings.
Submitted by Radib Kar, on June 12, 2020

Problem statement

Given 3 strings X, Y and Z, the task is to find the longest common sub-sequence in all three given sequences.

Input

Given input is the length of three string N, M, K and then in the next lines the strings X, Y, Z themselves respectively

Output

Print the length of the longest common sub- sequence of the three strings

Constraints

1<= N, M, K <=100

Example

Input:
N = 5, M = 6, K = 7

X = "inclu"
Y = "socluue"
Z = "anyclue"

Output:
The length of longest common subsequence for these three strings are 3

Explanation

The longest common subsequence for these three strings is:

"clu" which is of length 3

Solution Approach:

We need a 3D table to store the computed values.

Let's say for sub-sequences,

X[1...i] i < N
Y[1...j] j < M
Z[1...k] k < K

Now if X[i]==Y[j]==Z[k] then surely, we found a character which is common and we need to recur for the remaining ones

If they are not similar, we need to find maximum of three cases

1. Leave X[i] recur for others
2. Leave Y[j] recur for others
3. Leave Z[k] recur for others

So, if we formulate the above idea in to our recursion function then

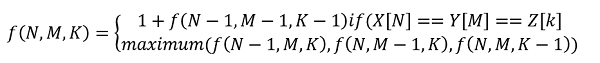
1. f(N-1,M,K) = Leave X[i] recur for others
2. f(N,M-1,K) = Leave Y[j] recur for others
3. f(N,M,K-1) = Leave Z[k] recur for others

Now, the above recursion will result to many overlapping sub problems. Hence, we need to convert the above to DP.

1. Initialize the dp table, dp[M+1][N+1][K+1]
2. Fill the base cases,

   for i=0 to M
       for j=0 to N
           dp[i][j][0]=0;
       end for
   end for
   for i=0 to N
       for j=0 to K 
           dp[0][i][j]=0;
       end for
   end for
   for i=0 to M
       for j=0 to K
           dp[i][0][j]=0;
       end for
   end for
   

3. Fill up the other values,

   for i=1 to M
       for j=1 to N
           for k=1 to K
               if(s1[i-1]==s2[j-1] && s2[j-1]==s3[k-1])
                   dp[i][j][k]=1+dp[i-1][j-1][k-1];
               else
                   dp[i][j][k]=max(dp[i-1][j][k],dp[i][j-1][k],dp[i][j][k-1]);
               end for
       end for
   end for
   

Obviously, visual illustration for the 3D DP calculation is not possible, but you can go through the computation for LCS between two strings to understand how this 3D table is being filled.

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int max(int a, int b, int c)
{

    if (a > b && a > c)
        return a;
    if (b > c)
        return b;
    return c;
}

int LCS3(string s1, string s2, string s3, int m, int n, int o)
{

    int dp[m + 1][n + 1][o + 1];

    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {
            dp[i][j][0] = 0;
        }
    }
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= o; j++) {
            dp[0][i][j] = 0;
        }
    }
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= o; j++) {
            dp[i][0][j] = 0;
        }
    }

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            for (int k = 1; k <= o; k++) {
                if (s1[i - 1] == s2[j - 1] && s2[j - 1] == s3[k - 1]) {
                    dp[i][j][k] = 1 + dp[i - 1][j - 1][k - 1];
                }
                else {
                    dp[i][j][k] = max(dp[i - 1][j][k], dp[i][j - 1][k], dp[i][j][k - 1]);
                }
            }
        }
    }
    return dp[m][n][o];
}

int main()
{
    int t, m, n, o;

    cout << "enter length of three strings respectively\n";
    cin >> m >> n >> o;

    cout << "enter the three strings respectively\n";
    string s1, s2, s3;
    cin >> s1 >> s2 >> s3;

    cout << "length of LCS of the three is : " << LCS3(s1, s2, s3, m, n, o) << endl;

    return 0;
}

Output

enter length of three strings respectively
5 6 7
enter the three strings respectively
inclu
socluu
anyclue
length of LCS of the three is : 3