Home » Interview coding problems/challenges

Floyd Warshall Algorithm

Floyd Warshall Algorithm: Here, we are going to learn how to find all pair shortest paths in any graph using Floyd Warshall Algorithm?
Submitted by Radib Kar, on January 10, 2020

Description:

This is a very popular interview problem to find all pair shortest paths in any graph. This problem has been featured in interview rounds of Samsung.

Problem statement:

Given a weighted directed graph, the problem is to find the shortest distances between every pair of vertices. The Graph is represented by an adjacency matrix, and any cell arr[i][j] denotes the weight of the edge (path cost) from node i to node j (if it exists) else INF.

Input: N=5

Adjacency matrix:

Example:

So the graph for the above input is,

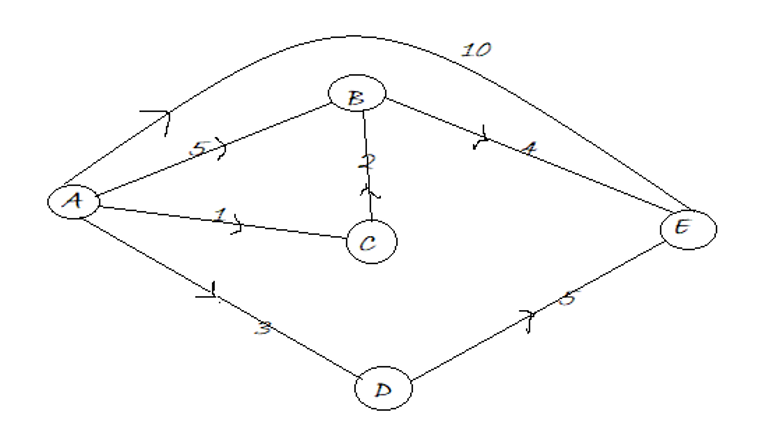
Figure 1: Directed Graph for which all pair shortest distance path needed to be found

    A → B: 5
    A → C: 1
    A → D: 3
    A → E: 10
    B → A: INF
    B → C: INF
    B → D: INF
    B → E: 4
    C → A: INF
    C → B: 2
    C → D: INF
    C → E: INF
    D → A: INF
    D → B: INF
    D → C: INF
    D → E: 5
    E → A: INF
    E → B: INF
    E → C: INF
    E → D: INF

Problem solution:

The Floyd Warshall algorithm computes the all pair shortest path in any weighted graph from the adjacency matrix. It also works for negative weight edges.

The algorithm is very simple to compute. Basically to compute the shortest path between i^th node to j^th node we check whether there is an intermediate node that reduces the distance, i.e., the path cost.

Let,

    D(i,j) = Distance from ith node to ith node

We check for whether there is any intermediate node, say v such that,

    D(i,u) + D(u,j) < D(i,j), for any intermidiate node u,uЄ[1,n]and u≠i,u≠j

Initially we consider the adjacency matrix to be the shortest distance table.

Based on this concept, the Floyd-Warshall algorithm is designed.

So, initially the shortest distance table is,

After updating the shortest distance from A to other nodes,

So on.

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

void FloydWarshal(long long int** arr, int n)
{
    for (int i = 0; i < n; i++) { //source node
        for (int j = 0; j < n; j++) { //destination node
            for (int k = 0; k < n; k++) { //intermediate node
                // if shortest path via the intermediate node exists
                if (arr[i][k] != INT_MAX && arr[k][j] != INT_MAX && arr[i][j] > arr[i][k] + arr[k][j])
                    arr[i][j] = arr[i][k] + arr[k][j]; //update shortest distance
            }
        }
    }

    cout << "Printing all pair shortest path distance\n";
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cout << char(i + 'A') << "->" << char(j + 'A') << ":";
            if (arr[i][j] == INT_MAX)
                cout << "INF"
                     << "\n";
            else
                cout << arr[i][j] << "\n";
        }
    }
}

int main()
{
    int n;
    string item;

    cout << "Number of node in the graph is:\n";
    cin >> n;
    long long int** arr = (long long int**)(malloc(sizeof(long long int*) * n));
    cout << "Enter the weights\n";

    //build the adjacency matrix
    for (int j = 0; j < n; j++) {
        arr[j] = (long long int*)(malloc(sizeof(long long int) * n));
        for (int k = 0; k < n; k++) {
            cout << "Enter weight of " << char(j + 'A') << " -> " << char(k + 'A') << endl;
            cin >> item;
            if (item == "INF")
                arr[j][k] = INT_MAX;
            else
                arr[j][k] = stoi(item);
        }
    }
    // function to compute all pair shortest distance
    FloydWarshal(arr, n);
    return 0;
}

Output

Number of node in the graph is:
5
Enter the weights
Enter weight of A -> A
0
Enter weight of A -> B
5
Enter weight of A -> C
1
Enter weight of A -> D
3
Enter weight of A -> E
10
Enter weight of B -> A
INF
Enter weight of B -> B
0
Enter weight of B -> C
INF
Enter weight of B -> D
INF
Enter weight of B -> E
4
Enter weight of C -> A
INF
Enter weight of C -> B
2
Enter weight of C -> C
0
Enter weight of C -> D
INF
Enter weight of C -> E
INF
Enter weight of D -> A
INF
Enter weight of D -> B
INF
Enter weight of D -> C
INF
Enter weight of D -> D
0
Enter weight of D -> E
5
Enter weight of E -> A
INF
Enter weight of E -> B
INF
Enter weight of E -> C
INF
Enter weight of E -> D
INF
Enter weight of E -> E
0
Printing all pair shortest path distance
A->A:0
A->B:3
A->C:1
A->D:3
A->E:7
B->A:INF
B->B:0
B->C:INF
B->D:INF
B->E:4
C->A:INF
C->B:2
C->C:0
C->D:INF
C->E:6
D->A:INF
D->B:INF
D->C:INF
D->D:0
D->E:5
E->A:INF
E->B:INF
E->C:INF
E->D:INF
E->E:0