Home » Interview coding problems/challenges

Print All Nodes that don't have Sibling

In this article, we are going to see how to find the nodes that have no siblings? This problem has been featured in the coding round of D.E. Shaw, Amazon. Submitted by Radib Kar, on December 17, 2018

Problem statement

Given a Binary Tree write a program to print the nodes which don’t have a sibling node. Print all the nodes separated by space which don't have sibling in the tree in sorted order if every node has a tree than print -1.

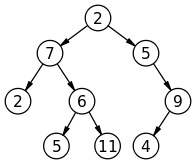
Explanation with example

What is having sibling in tree?

A child node is said to have a sibling if the other node has the same parent as the child node. That means the nodes are siblings if they have same parent.

Like in the above example ‘2’ & ‘6’ are siblings as they have the same parent ‘7’.

In the above example the nodes that don’t have siblings are: 9, 4

Thus output:

4, 9 (sorted)

N.B: Root is not considered for sibling checking.

Solution

So, clearly a child node don’t have sibling, if its parent has only one pointer, either left or the right (that’s the child of course). Then we simply store the child node value & produce a sorted list to print. The traversal method we use here is level order traversal.

Algorithm

1. Define tree Node structure
2. FUNCTION printSibling (Node* root)
    a) Declare a queue& a vector using STL 
    Queue<Node*>q;
    vector<int>store;
    b) push the root
    EnQueue(q,root);
    Node* temp;
    While(queue is not empty) //do the level order traversal & check for siblings
        temp=DeQueue(q);
        //if the current node has only one child, definitely the child 
        //has no sibling, thus store the child node value
        //left child pointer in NULL, right is not
        If temp->left==NULL&&temp->right!=NULL  
            Addtemp->right node value in store;
        END IF
        //right child pointer in NULL, left is not
        If temp->left!=NULL&&temp->right==NULL 
            Add temp->left node value in store;
        END IF
        // do level order traversing
        IF(temp->right)
        EnQueue(q, temp->right);
        IF(temp->left)
        EnQueue(q, temp->left);
    END WHILE
    c) If no node found without having sibling then vector size is zero then print -1
    d) Elsesort the vector to print sorted node value
END FUNCTION

C++ implementation to Print All Nodes that don't have Sibling

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class tree{    
	public:
		int data;
		tree *left;
		tree *right;
};

void printSibling(tree* root)
{
	//Declare queue using STL 
	queue<tree*> q;
	//enqueue the root
	q.push(root);
	vector<int> store;

	tree* temp;
	//do the level order traversal & check for siblings
	while(!q.empty()){
		//dequeue
		temp=q.front();
		q.pop();
		//if the current node has only one child 
		//definitely the child has no sibling
		//store the child node value
		if(temp->left==NULL && temp->right!=NULL){
			store.push_back(temp->right->data);
		}

		if(temp->left!=NULL && temp->right==NULL){
			store.push_back(temp->left->data);
		}
		// do level order traversing
		if(temp->right)
			q.push(temp->right);
		if(temp->left)
			q.push(temp->left);
	}
	//if no node found without having sibling
	//vector size is zero
	//print -1
	if(store.size()==0){
		printf("-1, no such  node\n");
	return;
	}
	//sort the vector to print sorted node value
	sort(store.begin(),store.end());
	//printing
	for(auto it=store.begin();it!=store.end();it++)
		printf("%d ",*it);
}

tree* newnode(int data)  // creating new node
{ 
	tree* node = (tree*)malloc(sizeof(tree)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 

	return(node); 
} 


int main() 
{ 
	//**same tree is builted as shown in example**
	cout<<"same tree is built as shown in example\n";
	tree *root=newnode(2); 
	root->left= newnode(7); 
	root->right= newnode(5); 
	root->right->right=newnode(9);
	root->right->right->left=newnode(4);
	root->left->left=newnode(2); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(5);
	root->left->right->right=newnode(11);

	cout<<"printing the nodes that don't have sibling...\n"<<endl; 
	printSibling(root);

	return 0; 
} 

Output

same tree is built as shown in example
printing the nodes that don't have sibling...

4 9