Home » Interview coding problems/challenges

Minimum Number of coins to make the change

Minimum Number of coins to make the change: Here, we are going to learn the solution to find minimum number of coins to make a change. Submitted by Radib Kar, on February 09, 2020

Description

This is classic dynamic programming problem to find minimum number of coins to make a change. This problem has been featured in interview rounds of Amazon, Morgan Stanley, Paytm, Samsung etc.

Problem statement

Given a value P, you have to make change for P cents, given that you have infinite supply of each of C { C₁, C₂, ... ,C_n} valued coins. Find the minimum number of coins to make the change. Return -1 if the change is not possible with the coins provided.

    Input:
    Amount P=13

    Coin values are:
    1, 4, 5 
    
    Output:
    3

Explanation with example

Let's solve the above example. Total amount is 13 and we have coins with values 1, 4 and 5.

Since, we are to find minimum number of coins and we have infinite number of coin for any denomination, it's apparent that we would go for greedy. We should pick the coin with maximum denomination and keep trying with that until the remaining amount of the change is less the denomination of the coin. Then on course we keep choosing the next best one. So, the algorithm would be like.

    1) Let, count=0 to count minimum number of coin used
    2) Pick up coin with maximum denomination say, value x
    3) while amount≥x
            amount=amount-x
            count=count+1 

    4) if amount=0
            Go to Step 7
    5) Pick up the next best denomination of coin and assign it to x
    6) Go to Step 2
    7) End. count is the minimum number of coin used.

Let's see whether the above greedy algorithm leads to the desired result or not.

    So, we would pick up 5 first from {1, 4, 5}
    We would pick 5 two times
    Now amount=3, count=2
    Next best coin is 4 but 4 > amount
    Next best coin is 1
    We would pick 1 three times
    Amount=0 and count=5
    So, minimum number of coins needed for the change is 5.

    But is it really minimum?
    If we choose one coin with denomination 5 and two coins with denomination 4, 
    it would make the change and coins needed here is (2+1) = 3 
    So, greedy does not work as the local optimum choices doesn't make 
    global optimum choice. Hence, we need dynamic programming.

Problem Solution Approach

We have amount M and n number of coins, {C₁, C₂, ..., C_n}

Now,

We have two choice for any C_j,

1. Use C_j and recur for amount M-C_j
2. Don't use C_j and recur for amount M with other coins

(m)= minimum number of coins needed to change amount m

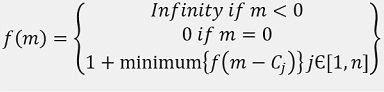
We can formulate the above recursion using DP.

    // (for any amount 0 to M, minimum number of coins needed is initially infinity) 
    1) Initialize DP[M+1] with INT_MAX. 
    2) DP[0]=0 //base case of above recursion
    3)  for  i=1 to M //iterate amounts
            for any coin C_j
                If i>=C_j  && DP[i-C_j]≠INT_MAX && DP[i-C_j]+1<DP[i])
                DP[i]=DP[i-C_j]+1; //update value
            End for
        End for   
    
    The result is DP[M]

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int coin_change(vector<int> a, int m, int n)
{

    //////////////////recursive implementation//////////////
    // if(m<0)
    // return;
    // if(m==0){
    //     if(count<min_count)
    //     min_count=count;
    //     return;
    // }

    // for(int i=0;i<n;i++){
    //     coin_change(a,i,m-a[i],n,count+1);
    //     coin_change(a,i+1,m-a[i],n,count+1);
    // }

    ///////////DP implementation///////////////
    //base value
    int DP[m + 1];
    //initialize
    for (int i = 1; i <= m; i++)
        DP[i] = INT_MAX;
    DP[0] = 0;
    for (int i = 1; i <= m; i++) {
        for (int j = 0; j < n; j++) {
            // if amount > coin value
            if (i >= a[j] && DP[i - a[j]] != INT_MAX && DP[i - a[j]] + 1 < DP[i])
                // if updation possible update for minimum value
                DP[i] = DP[i - a[j]] + 1;
        }
    }

    return DP[m];
}
int main()
{
    int n, item, m;

    cout << "Enter amount to be changes:\n";
    cin >> m;
    cout << "Enter number of coins:\n";
    cin >> n;
    cout << "Enter coin values\n";
    vector<int> a;
    for (int j = 0; j < n; j++) {
        scanf("%d", &item);
        a.push_back(item);
    }
    int ans = coin_change(a, m, n);
    if (ans == INT_MAX)
        cout << "Coin change not possible" << endl;
    else
        cout << "Minimum number of coins needed: " << ans << endl;

    return 0;
}

Output

RUN 1:
Enter amount to be changes:
13
Enter number of coins:
3
Enter coin values
1 4 5
Minimum number of coins needed: 3

RUN 2:
Enter amount to be changes:
11
Enter number of coins:
2
Enter coin values
4 5
Coin change not possible