Home » Interview coding problems/challenges

Minimum number of deletions to make a sorted sequence

Minimum number of deletions to make a sorted sequence: In this article, we are going to see how to solve this problem which already featured in interview rounds of Amazon?
Submitted by Radib Kar, on June 07, 2020

Problem statement

Given an array of n integers. Find the minimum number of elements from the array to remove or delete so that when the remaining elements are placed in the same sequence order form a sorted sequence.

Input

First line contains size N.
Next line contains N input elements for the array

Output

Output the minimum number of deletions to make a sorted sequence.

Constraints:

1<= N <=1000
1<= A[i ] <=1000

Example

Input:
5
5 8 5 5 4

Output:
1

Explanation:
The longest increasing subsequence is: (not strictly increasing)
5, 8 or 5,5

So we need to remove minimum three characters
The longest decreasing subsequence is: (not strictly increasing)
8 5 5 4

So we need to remove minimum one character

Thus the final output is 1
And the sorted sequence is the decreasing one
8 5 5 4 

Solution Approach

So, for the sequence to be sorted we need to check for both the longest increasing and decreasing subsequence.

Let,

Longest increasing subsequence be known as LIS and Longest decreasing subsequence is LDS

So minimum elements to be deleted= array length- maximum(LIS, LDS)

Intuitively, the minimum value of maximum(LIS, LDS) would be 1 as each element represents the primitive sequence which is either increasing or decreasing one.

So, the base value is 1.

Now,

Lis(i)=longest increasing subsequence starting from index 0 to index i
Lds(i)=longest decreasing subsequence starting from index 0 to index i 

So,

To compute LIS(i), LDS(i) the recursion function is,

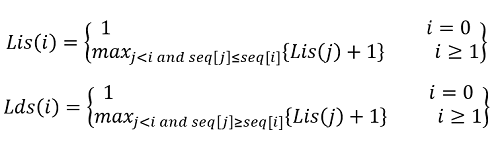
As, the base value is 1, for every index i, Lis(i), Lds(i) is at least 1.

1)  Create two DP array, Lis[n],Lds[n]
2)  Initialize both the DP array with 1.
        for i=0 to n-1
            Lis[i]=1,Lds[i]=1;
3)  Now, to compute the Lis[i],Lds[i]
        for index  i=1 to n-1         
            for previous index j=0 to i-1
                //if (arr[i],arr[j]) is inceasing sequence
                if(lis[i]<lis[j]+1 &&a[i]≥a[j])
                    lis[i]=lis[j]+1;
                //if (arr[i],arr[j]) is deceasing sequence
                if(lds[i]<lds[j]+1 &&a[i]≤a[j])
                    lds[i]=lds[j]+1;
            end for
        end for 

Now, Minimum elements to be deleted =

n-maximum(maximum value in (lds),maximum value in (lis))

To go through detailed explanation on LIS go through previous article on LIS: Longest Increasing Subsequence

LDS is quite similar like LIS, follow the recursion for LDS to understand this too.

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int LIDS(vector<int> arr, int n)
{

    int LIS[n], LDS[n];

    for (int i = 0; i < n; i++)
        LIS[i] = 1;
    for (int i = 0; i < n; i++)
        LDS[i] = 1;

    int maxi = INT_MIN, maxd = INT_MIN;

    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            // for longest increasing sequence
            if (arr[i] >= arr[j] && LIS[i] < LIS[j] + 1)
                LIS[i] = LIS[j] + 1;

            // for longest decreasing sequence
            if (arr[i] <= arr[j] && LDS[i] < LDS[j] + 1)
                LDS[i] = LDS[j] + 1;
        }
        //find maximum longest s orted sequence
        if (LIS[i] > maxi)
            maxi = LIS[i];

        if (LDS[i] > maxd)
            maxd = LDS[i];
    }

    return std::max(maxi, maxd);
}

int main()
{
    int t, n, item;
    cout << "Enter n:\n";
    scanf("%d", &n);
    cout << "Enter the array\n";
    vector<int> a;
    for (int j = 0; j < n; j++) {
        scanf("%d", &item);
        a.push_back(item);
    }

    cout << "Minimum elements needed to be deleted to create sorted sequence: " << n - LIDS(a, n) << endl;

    return 0;
}

Output

Enter n:
5
Enter the array
5 8 5 5 4
Minimum elements needed to be deleted to create sorted sequence: 1