Home » Interview coding problems/challenges

Knight walk problem

Knight walk problem: In this article, we are going to learn how to solve the knight walk problem using C++ program?
Submitted by Souvik Saha, on May 11, 2019

Problem Statement:

There is a chessboard of size N×M and starting position (sx, sy) and destination position (dx,dy). You have to find out how many minimum numbers of moves a knight goes to that destination position?

Example:

Input:

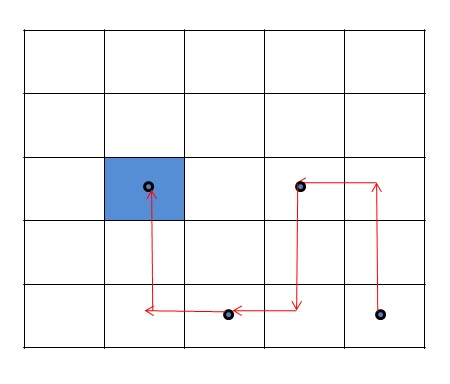
Check the above example...

If the source position is (5,5) and the destination position is (3,2).
Then the path count is 3.

Algorithm:

To solve this problem we follow this approach:

1. We use queue data structure and initialize it with the starting position and a map data structure to count the steps where the key is position and value is step count.
2. Then we pop the top position and push all the possible positions that are reached from that position (a knight moves 2 steps at any direction and then one step left or right) and increase the step count of the popped position by one.
3. We repeat step 2 until we reach the destination position and the first value is the minimum value.

C++ Implementation for Knight walk problem

#include <bits/stdc++.h>
using namespace std;

int num_x[] = { -2, -2, -1, 1, 2, 2, 1, -1 };
int num_y[] = { -1, 1, 2, 2, 1, -1, -2, -2 };

bool isvalid(int r, int c, int row, int col)
{
    return (row >= 0 && row < r && col >= 0 && col < c);
}

int count(int r, int c, int sx, int sy, int dx, int dy)
{
    queue<pair<pair<int, int>, int> > q;
    set<pair<int, int> > st;
    q.push(make_pair(make_pair(sx, sy), 0));
    while (!q.empty()) {
        pair<pair<int, int>, int> p = q.front();
        st.insert(make_pair(sx, sy));
        if (p.first.first == dx && p.first.second == dy) {
            return p.second;
        }
        q.pop();
        for (int i = 0; i < 8; i++) {
            int row = p.first.first + num_x[i];
            int col = p.first.second + num_y[i];
            if (isvalid(r, c, row, col) && st.find(make_pair(row, col)) == st.end()) {
                st.insert(make_pair(row, col));
                int temp = p.second + 1;
                q.push(make_pair(make_pair(row, col), temp));
            }
        }
    }
    return -1;
}

int main()
{
    int r, c;
    cout << "Row: ";
    cin >> r;
    cout << "Col: ";
    cin >> c;
    int sx, sy, dx, dy;
    cout << "Staring position : ";
    cin >> sx >> sy;
    cout << "Destination position : ";
    cin >> dx >> dy;
    cout << "Steps :";
    cout << count(r, c, sx - 1, sy - 1, dx - 1, dy - 1) << endl;
    return 0;
}

Output

Row: 5
Col: 5
Staring position : 5 5
Destination position : 3 2
Steps :3