Home » Interview coding problems/challenges

Partition a set into k subset with equal sum

Partition a set into k subset with equal sum: Here, we are going to learn to make partitions for k subsets each of them having equal sum using backtracking.
Submitted by Souvik Saha, on February 04, 2020

Description:

This is a standard interview problem to make partitions for k subsets each of them having equal sum using backtracking.

Problem statement:

A set is given. You have to make K subsets by which all of the subsets have equal sum.

    Test case T
    // T no. of line with the value of N and corresponding values and the value of K.
    
    E.g.
    2
    
    29
    71 69 9 16 41 50 97 24 19 46 47 52 22 56 80 89 65 29 42 51 94 1 35 65 25 15 88 57 44 
    2

    15
    29 28 51 85 59 21 25 23 70 97 82 31 85 93 73 
    3
    
    Constraints:
    1<=T<=100
    1<=N,K<=100
    1<=Set[] <=100
    
    Output:
    Print T lines either Partition possible or Partition is not possible.

Example

    Input:
    N=15
    Set[]= { 29 28 51 85 59 21 25 23 70 97 82 31 85 93 }
    K=3
    
    Then the subsets are:
    {85,21,23,70,85}
    {28,59,31,93,73}
    {29,51,25,97,82}

    Output:
    Partition possible

Explanation with example

Let there is a set of N positive numbers X₁, X₂, X₃, ..., X_n.

To make K no. of subset with equal sum is a problem of combination and we solve it using backtracking. We will follow some possible path to solve this problem.

1. If the K equals to 1 then it always true and the value of K is greater than N then it is impossible so it is false then.
2. We will sum up all the values 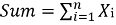and divide the Sum by K.
3. If the sum is fully divisible by k then we will go to the step 4 otherwise it is false.
4. We will take a Boolean array to identify the values which are already been used.
5. Firstly, we will go for the first subset which has the sum equals to (Sum/K) and make the mark which of the elements are taken consideration.
6. After getting the first subset we will go for the other but in that case will not consider the numbers which are already been used for the first subset and those are indicated by the Boolean array.
7. For the last subset will not go for the search because all the remaining numbers must have the sum equals to (Sum/K).

For the input,

    N = 15
    Set[] = { 29 28 51 85 59 21 25 23 70 97 82 31 85 93 }
    K = 3

Firstly, we calculate the total Sum = 779 and K = 3. So, 779 is divisible by 3.

Then we will choose any of the value from starting and start our backtracking algorithm according to that and find the subsets with equal sum,

    {85,21,23,70,85}
    {28,59,31,93,73}
    {29,51,25,97,82}

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

bool is_partiable(int* arr, int n, int sum, int curr_sum, bool* visited, int pos)
{
    if (curr_sum == sum) {
        return true;
    }

    if (pos >= n || pos < 0) {
        return false;
    }

    for (int i = pos; i >= 0; i--) {
        //take the elements those are not visited
        if (!visited[i]) {
            visited[i] = true;
            if (curr_sum + arr[i] <= sum && is_partiable(arr, n, sum, curr_sum + arr[i], visited, i - 1)) {
                return true;
            }
            visited[i] = false;
        }
    }
    return false;
}

bool isKPartitionPossible(int A[], int N, int k)
{
    int sum = 0;

    for (int i = 0; i < N; i++) {
        sum += A[i];
    }

    if (sum % k != 0)
        return false;

    sum = sum / k;

    bool visited[N];

    memset(visited, false, sizeof(visited));

    for (int i = 0; i < k - 1; i++) {
        int curr_sum = 0;
        int pos = N - 1;
        if (!is_partiable(A, N, sum, curr_sum, visited, pos))
            return false;
    }

    return true;
}

int main()
{
    int t;

    cout << "Test Case : ";
    cin >> t;

    while (t--) {
        int n;

        cout << "Enter the value of n : ";
        cin >> n;

        int arr[n];

        cout << "Enter the numbers : ";
        for (int i = 0; i < n; i++) {
            cin >> arr[i];
        }

        int k;

        cout << "Enter the value of K : ";
        cin >> k;

        if (isKPartitionPossible(arr, n, k)) {
            cout << "Partition possible" << endl;
        }
        else {
            cout << "Partition is not possible" << endl;
        }
    }
    return 0;
}

Output

Test Case : 2

Enter the value of n : 29
Enter the numbers : 71 69 9 16 41 50 97 24 19 46 47 52 22 56 80 89 65 29 42 51 94 1 35 65 25 15 88 57 44
Enter the value of K : 2
Partition is not possible

Enter the value of n : 15
Enter the numbers : 29 28 51 85 59 21 25 23 70 97 82 31 85 93 73
Enter the value of K : 3
Partition possible