Home » Interview coding problems/challenges

Longest Increasing Subsequence

Longest Increasing Subsequence: Here, we are going to learn about the solution of one of the most popular dynamic programming problems often used as building block to solve other problems.
Submitted by Radib Kar, on February 08, 2020

Description:

This is one of the most popular dynamic programming problems often used as building block to solve other problems.

Problem statement:

Given a sequence A of size N, find the length of the longest increasing subsequence from the given sequence.

The longest increasing subsequence means to find a subsequence of a given sequence where the subsequence's elements are sorted in increasing order, and the subsequence is longest possible. This subsequence is not necessarily contiguous, or unique. Longest increasing subsequence is strictly increasing.

    Input:
    N=7
    Sequence:
    {2, 3, 4, 0, 1, 2, 3, 8, 6, 4}

    Output:
    Length of Longest increasing subsequence is 5
    Longest increasing subsequence= {0, 1, 2, 3, 8} or {0, 1, 2, 3, 4}

Explanation with example

The possible increasing sub-sequences are,

Of Length 1 //each element itself is an increasing sequence

So, on...

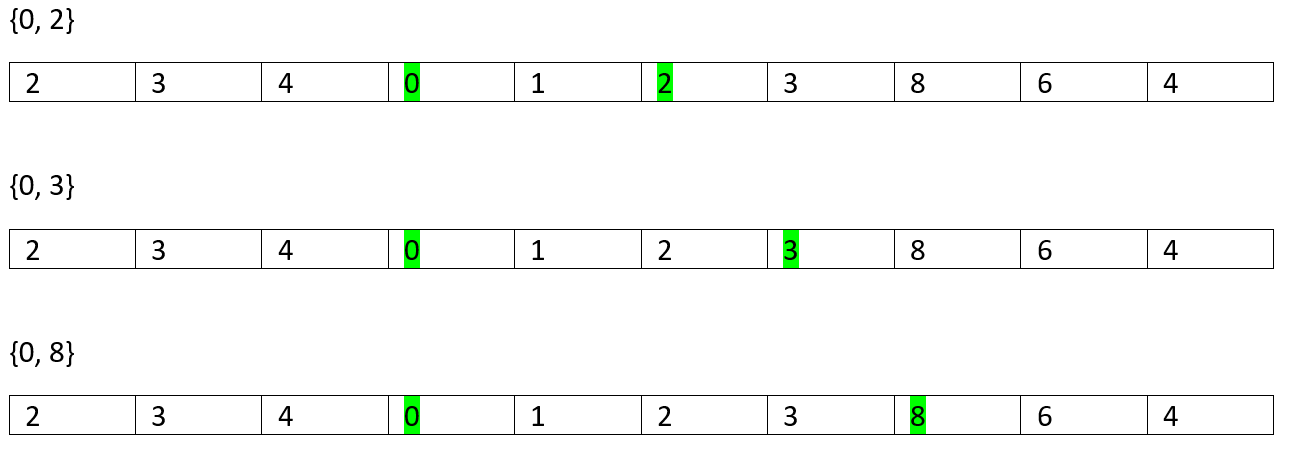
So, on...

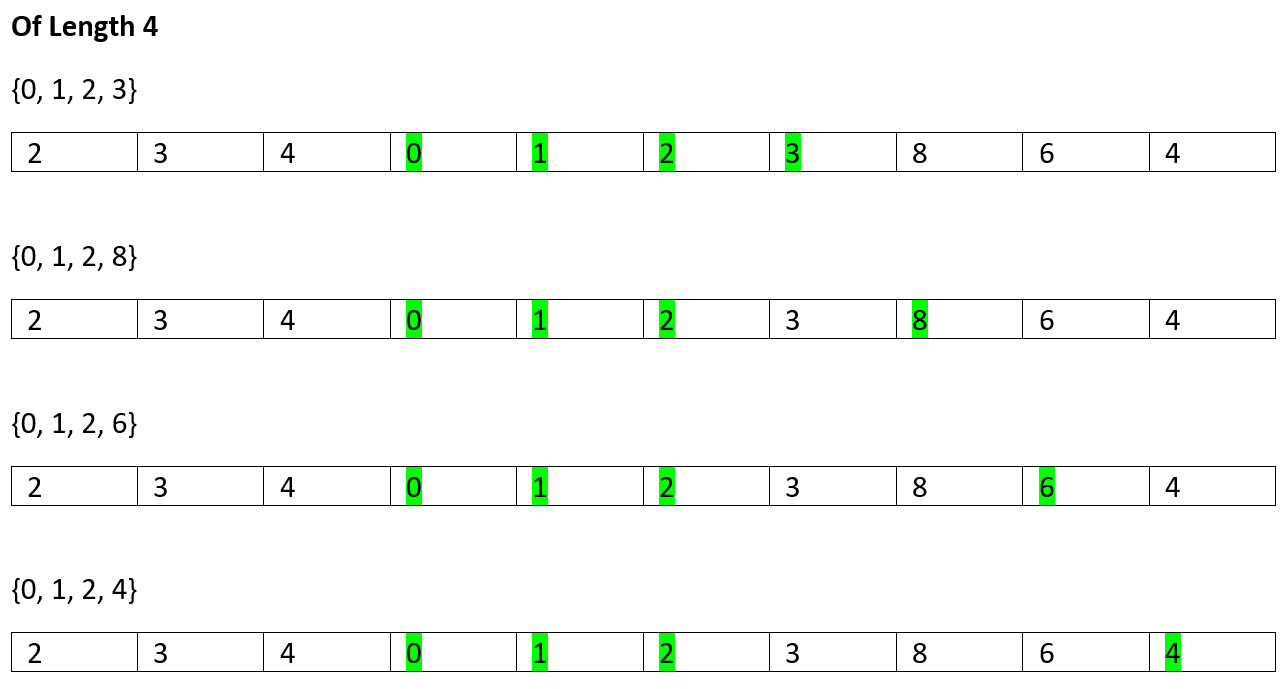
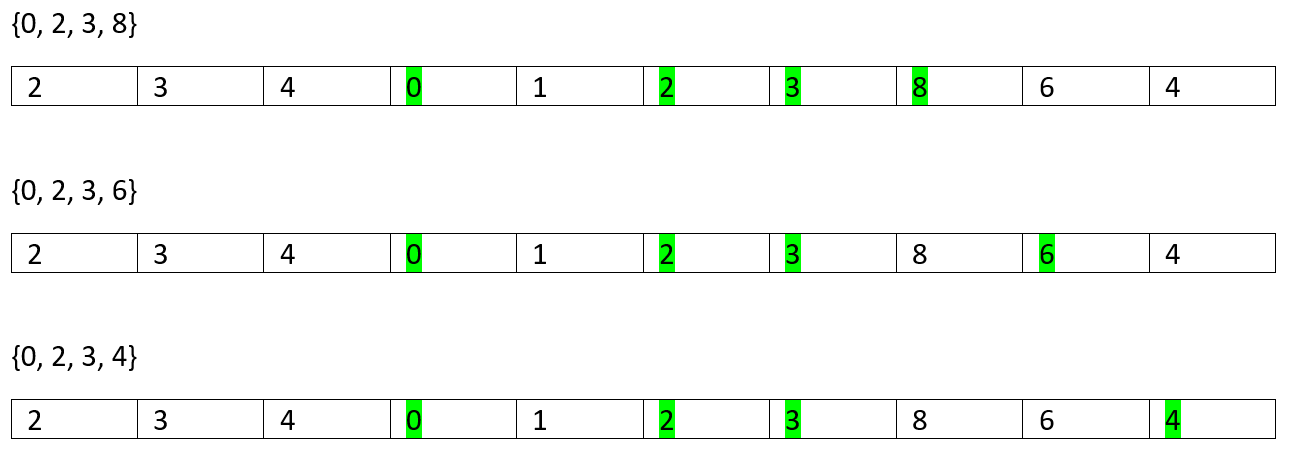
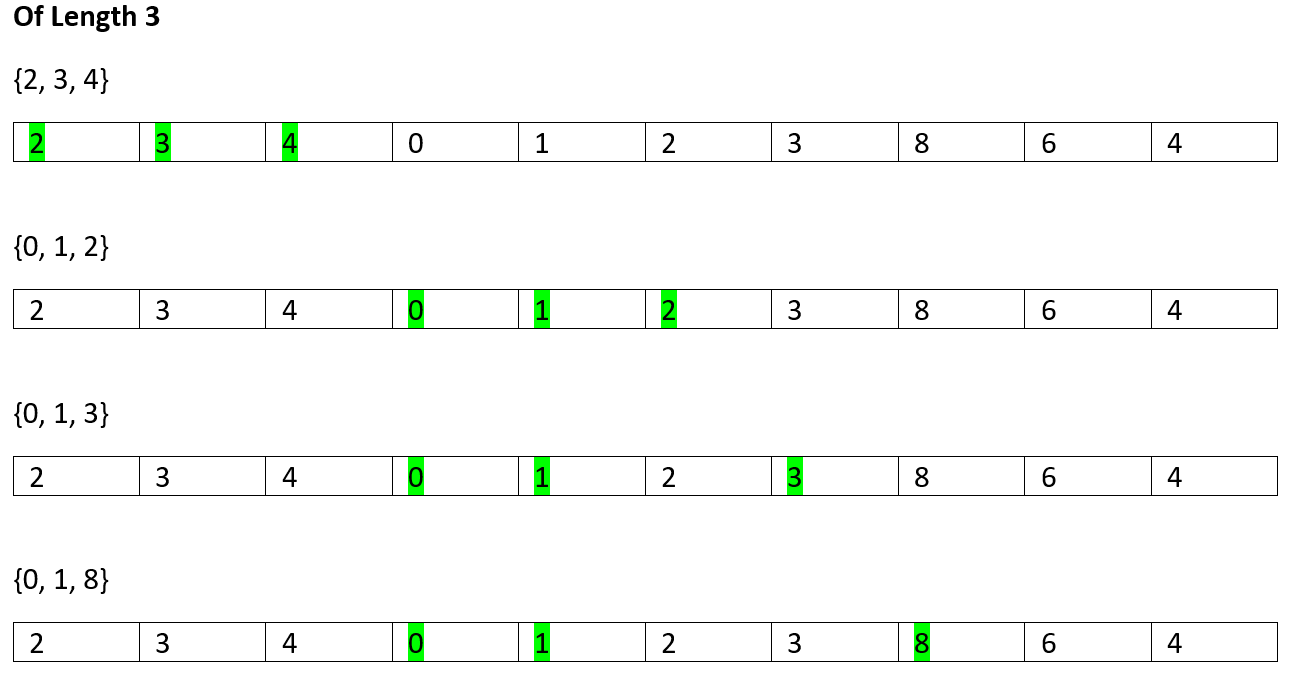
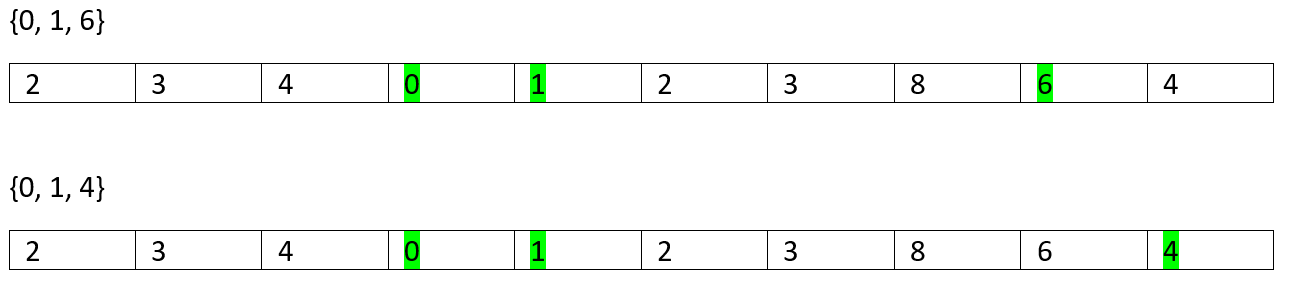
So, on...

No more
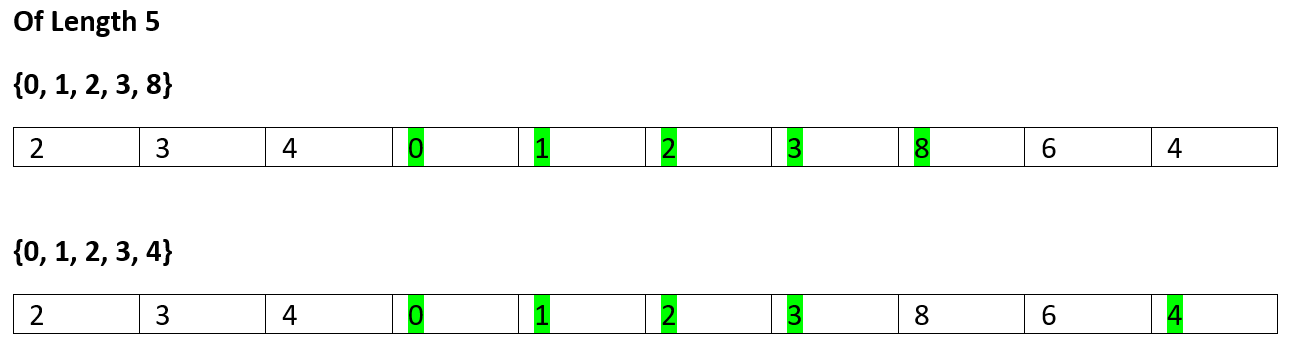
Of Length 6
None

So, the longest increasing subsequence length is 5.

Problem Solution Approach

Of course, in brute-force we can simply generate all increasing sequences and find the longest one. But it would take exponential time which is not a feasible solution. Hence, we choose Dynamic programming to solve.

We create a DP table to store longest increasing subsequence length.
It's intuitive that the minimum value would be 1 as each element represents the primitive sequence which is an increasing one.

So, the base value is 1.

Now,

    Lis(i) = longest increasing subsequence starting from index 0 to index i

So,
To compute L(i) the recursion function is,

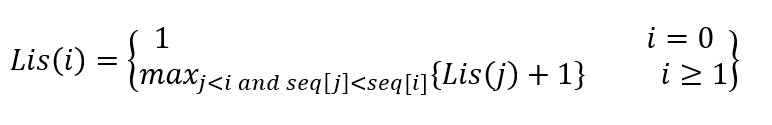
As, the base value is 1, for every index i, L(i) is at least 1.

    
    1) Create the DP array, Lis[n]
    2) Initialize the DP array.
        for i=0 to n-1
            lis[i]=1;
    3) Now, to compute the Lis[i]
    for index  i=1 to n-1         
        for previous index j=0 to i-1
            // if (arr[i],arr[j]) is inceasing sequence
            if(lis[i]<lis[j]+1 && a[i]>a[j])
                lis[i]=lis[j]+1;
        end for
    end for 

Initially DP table,

So, the maximum out of this is 5
Hence, LIS=5.

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

int max(int a, int b)
{
    if (a > b)
        return a;
    else
        return b;
}

int LIS(vector<int> a, int n)
{
    int lis[n];

    //base case
    for (int i = 0; i < n; i++)
        lis[i] = 1;

    //fill up table
    for (int i = 1; i < n; i++) {

        for (int j = 0; j < i; j++) {
            if (lis[i] < lis[j] + 1 && a[i] > a[j])
                lis[i] = lis[j] + 1;
        }
    }
    //return LIS
    return *max_element(lis, lis + n);
}
int main()
{
    int n, item;

    cout << "Sequence size:\n";
    scanf("%d", &n);
    //input the array
    vector<int> a;
    cout << "Input sequence:\n";
    for (int j = 0; j < n; j++) {
        scanf("%d", &item);
        a.push_back(item);
    }

    cout << "Length of longest incresing subsequence is: " << LIS(a, n) << endl;

    return 0;
}

Output

Sequence size:
10
Input sequence:
2 3 4 0 1 2 3 8 6 4
Length of longest incresing subsequence is: 5