Home » Interview coding problems/challenges

Count total number of Palindromic Substrings

Count total number of Palindromic Substrings: Here, we are going to see how to find the total number of Palindromic substrings in a string? This is a standard interview problem that can be featured in any interview coding rounds and also got featured in the amazon interview.
Submitted by Radib Kar, on June 15, 2020

Problem statement:

Given a string str, find total number of possible palindromic sub-sequences. A substring need to be consecutive such that for any x_ix_j i<j must be valid in the parent string too. Like "incl" is a substring of "includehelp" while "iel" is not.

Input:

The first line of input contains an integer T, denoting the no of test cases then T test cases follow. Each test case contains a string str.

Output:

For each test case output will be an integer denoting the total count of palindromic substring which could be formed from the string str.

Constraints:

1 <= T <= 100
1 <= length of string str <= 300

Example:

Input:
test case:2

First test case:
Input string:
"aaaa"

Output:
Total count of palindromic substring is: 10

Second test case:
Input string:
"abaaba"

Output:
Total count of palindromic sub-sequence is: 11

Explanation:

Test case 1: Input: "aaaa"

The valid palindromic sub-sequences are shown below:

Marked cells are character taken in subsequence:

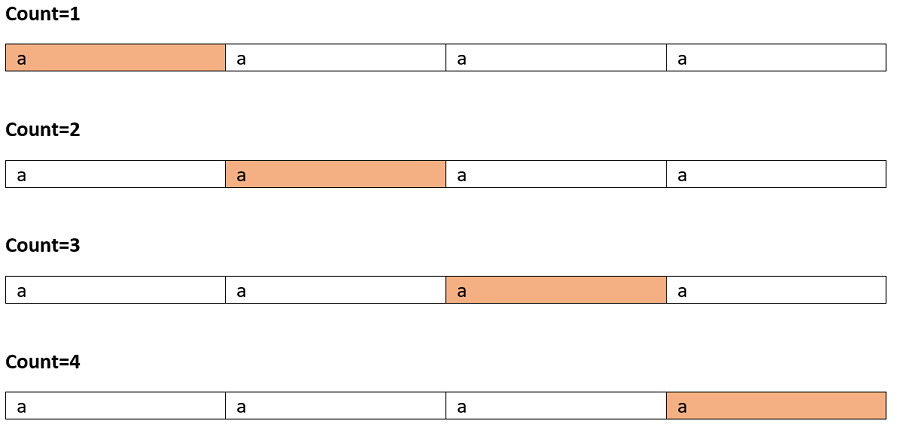
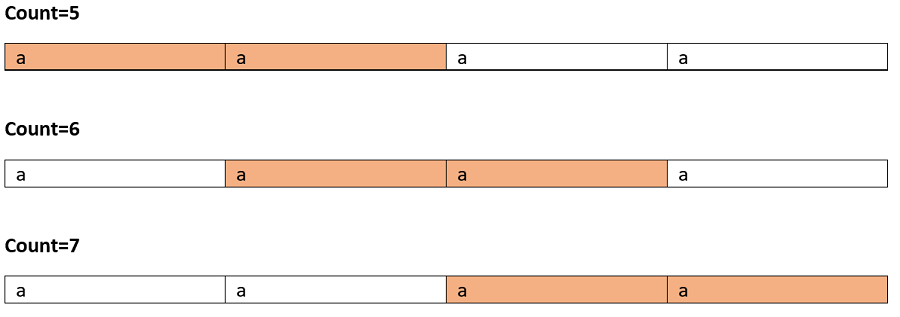
So on...

Total 10 palindromic substrings.

Actually in this case since all the character is same each and every substring is palindrome here.

For the second test case,

Few substrings can be,
"a"
"b"
"a"
"aba"

So on...

Total 11 such palindromic sub sequences

Solution approach

This can be solved by using DP bottom up approach,

1. Initialize dp[n][n] where n be the string length to 0 and a Boolean 2D array pal[n][n] to store whether the substrings are palindrome or not.
2. Fill up the base case,
   Base case is that each single character is a palindrome itself. And for length of two, i.e, if adjacent characters are found to be equal then [i][i+1]=3, pal[i][i+1]=true, else if characters are different then dp[i][i+1]=2, pal[i][i+1]=false
   To understand this lets think of a string like "acaa"
   Here, dp[0][1]=2 because there's only two palindrome possible because of "a" and "c".
   Whereas for dp[2][3] value will be 3 as possible substrings are "a", "a", "aa".

   for i=0 to n
   	// for single length characters
   	dp[i][i]=1;pal[i][i]=true 
   	if(i==n-1)
   		break;        
   	if(s[i]==s[i+1])
   		dp[i][i+1]=3;,pal[i][i+1]=true
   	else
   		dp[i][i+1]=2,pal[i][i+1]=false;
   	end if
   end for
   

3. Compute for higher lengths,

   for len=3 to n
   	for start=0 to n-len
   		int end=start+len-1;
   		// start and end is matching and rest of 
   		// substring is already palindrome
   		if(s[end]==s[start]  and pal[start+1][end-1]) 
   			// 1+subsequence from semaining part
   			dp[start][end]=1+dp[start+1][end]+dp[start][end-1]-dp[start+1][end-1]; 
   			Pal[start][end]=true;
   		else
   			dp[start][end]=dp[start+1][end]+dp[start][end-1]-dp[start+1][end-1];
   			Pal[start][end]=false;
   		end if
   	end for
   end for
   

4. Final result is stored in dp[0][n-1];

So for higher lengths if starting and ending index is same then we recur for the remaining characters, since we have the sub-problem result stored so we computed that. In case start and end index character are different then we have added dp[start+1][end] and dp[start][end-1] that's similar to recur for leaving starting index and recur for leaving end index. But it would compute dp[start+1][end-1] twice and that why we have deducted that.

For proper understanding you can compute the table by hand for the string "aaaa" to understand how it's working.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

int countPS(string s)
{

    int n = s.length();

    if (n == 0 || n == 1)
        return n;

    vector<vector<int> > dp(n);
    vector<vector<bool> > pal(n);

    for (int i = 0; i < n; i++) {
        dp[i] = vector<int>(n);
        pal[i] = vector<bool>(n);
    }

    for (int i = 0; i < n; i++) {
        dp[i][i] = 1;
        pal[i][i] = true;
        if (i == n - 1)
            break;
        if (s[i] == s[i + 1]) {
            dp[i][i + 1] = 3;
            pal[i][i + 1] = true;
        }
        else {
            dp[i][i + 1] = 2;
            pal[i][i + 1] = false;
        }
    }
    for (int len = 3; len <= n; len++) {
        for (int start = 0; start <= n - len; start++) {
            int end = start + len - 1;
            if (s[start] == s[end] && pal[start + 1][end - 1]) {
                dp[start][end] = dp[start + 1][end] + dp[start][end - 1] - dp[start + 1][end - 1] + 1;
                pal[start][end] = true;
            }
            else {
                dp[start][end] = dp[start + 1][end] + dp[start][end - 1] - dp[start + 1][end - 1];
                pal[start][end] = false;
            }
        }
    }
    return dp[0][n - 1];
}

int main()
{
    int t;

    cout << "Enter number of testcases\n";
    cin >> t;

    while (t--) {
        string str;

        cout << "Enter number of strings\n";
        cin >> str;

        cout << "Number of total palindromic substring is: " << countPS(str) << endl;
    }

    return 0;
}

Output:

Enter number of testcases
2
Enter number of strings
aaaa
Number of total palindromic substring is: 10
Enter number of strings
abaaba
Number of total palindromic substring is: 11