Home » Interview coding problems/challenges

Minimum steps to minimize n as per given condition

Minimum steps to minimize n as per given condition: Here, we are going to see how to solve a recursion problem efficiently by memorization.
Submitted by Radib Kar, on June 13, 2020

Problem statement

Given a number n, count minimum steps to minimize it to 1 performing the following operations:

1. Operation1: If n is divisible by 2 then we may reduce n to n/2.
2. Operation2: If n is divisible by 3 then you may reduce n to n/3.
3. Operation3: Decrement n by 1.

Input

Input is a single integer, n.

Output

Output the minimum number of steps to minimize the number performing only the above operations.

Constraints:

1 <= N <= 10000

Example

Test case 1:
Input:
N=10

Output:
Minimum number of steps needed: 3

Test case 2:
Input:
N=6

Output:
Minimum number of steps needed: 2

Explanation

For the above test case,
N=10

N is not divisible by 3, but by 2
So,
10->5
Now % is again neither divisible by 3 nor 2
So, only option is to decrement

Hence
5->4
4 can be decremented to 2 by dividing by 2
4->2
2->1

So,
The conversion path will be
10->5->4->2->1
Total 4 steps
But is this the optimal one?
Answer is no

The optimal will be
10 converted to 9 by decrementing
10->9
9->3->1

So, total of 3 steps which is the minimum number

Hence answer would be 3

Solution Approach

The above problem is a classic recursion example.

Like,

1. If n is divided by both 2 and 3
   Recur for possibilities (n/3), (n/2), (n-1)
2. If n is divided by only 3 but not by 2 then
   Recur for possibilities (n/3), (n-1)
3. If n is divided by only 2 but not by 3 then
   Recur for possibilities (n/2), (n-1)
4. If n is divided by only 3 but not by 2 then
   Recur for possibilities (n/3), (n-1)
5. If n is not divisible by both 2 and 3
   Then only recur for (n-1)

We can write all this with help of recursive function,

Let,
f(n) = the minimum number of steps to convert n to 1

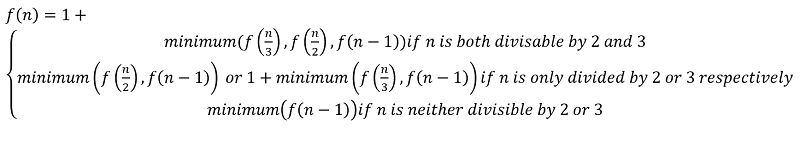
If you draw the recursion tree for f(10) you will find many overlapping sub-problems. Hence, we need to store all the already computed sub-problems through memorization.

Function minimumSteps(n)
    if(n==1)
        return 0;
    
    // memoization here, no need to compute if already computed
    if(dp[n]!=-1) 
        return dp[n];
    // store if not computed
    if(n%3==0 && n%2==0)
        dp[n]=1+min(minimumSteps(n-1),min(minimumSteps(n/3),minimumSteps(n/2)));
    else if(n%3==0)
        dp[n]=1+min(minimumSteps(n-1),minimumSteps(n/3));  
    else if(n%2==0)
        dp[n]=1+min(minimumSteps(n-1),minimumSteps(n/2)); 
    else
        dp[n]=1+minimumSteps(n-1);
    end if
    return dp[n]
End Function

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int dp[10001];

int minimumSteps(int n)
{

    if (n == 1)
        return 0;

    if (dp[n] != -1)
        return dp[n];

    if (n % 3 == 0 && n % 2 == 0) {
        dp[n] = 1 + min(minimumSteps(n - 1), min(minimumSteps(n / 3), minimumSteps(n / 2)));
    }
    else if (n % 3 == 0) {
        dp[n] = 1 + min(minimumSteps(n - 1), minimumSteps(n / 3));
    }
    else if (n % 2 == 0) {
        dp[n] = 1 + min(minimumSteps(n - 1), minimumSteps(n / 2));
    }
    else
        dp[n] = 1 + minimumSteps(n - 1);

    return dp[n];
}

int main()
{
    int n, item;

    cout << "enter the initial number, n \n";
    cin >> n;

    for (int i = 0; i <= n; i++)
        dp[i] = -1;

    cout << "Minimum number of steps: " << minimumSteps(n) << endl;

    return 0;
}

Output

RUN 1:
enter the initial number, n 
15
Minimum number of steps: 4

RUN 2:
enter the initial number, n 
7
Minimum number of steps: 3