Home » Interview coding problems/challenges

Check whether a Binary Tree is BST (Binary Search Tree) or not

Here, we are going to learn how to check whether a give binary tree is a binary search tree (BST) or not?
Submitted by Radib Kar, on November 25, 2018

Description:

This article describes how to check whether a given tree is BST or not? This problem came in coding round of Microsoft.

Problem Statement:

Given a binary tree check whether it is a binary search tree or not.

Solution

Algorithm:

From the definition of BST, it may seem that for a binary tree to be BST, it’s enough to check for each node if the node on its left is smaller & node on its right is greater. But this is actually the wrong approach since it will give wrong output for many test-cases.

The correct algorithm is to check for each node whether the maximum of the left subtree is lesser than the node & the minimum of the right subtree is greater than the node. This algorithm works perfect but not efficient in terms of time complexity.

Intuition says that the in-order traversal for the BST results in a sorted list of nodes and we use this in our algorithm.

1.  Set prev to INT_MIN.
2.  From main function call checkBST(root, prev)
    //passing prev by reference to update it every time
    checkBST(root, &prev) 
3.  if(root==NULL) 
        return 1; //null tree is BST
4.  do in-order traversal and checking whether all tree node 
    data is sorted or not
    if(!(checkBST(root->left,prev)))  //check left subtree 
        return 0;
    //root->data must be greater than prevsince BST results in 
    //sorted list after in-order traversal.
5.  if(root->data<prev) 
        return 0;
6.  prev=root->data; //update prev value
7.  return checkBST(root->right,prev);//check right subtree

Example 1:

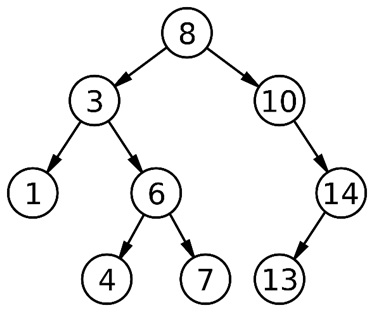
Clearly Example 1 is a binary search tree. We will check out further through our function.

Example 2:

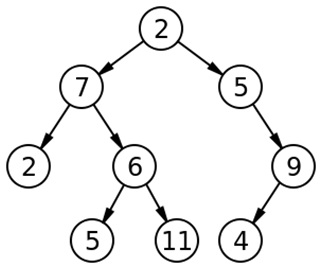
Clearly Example 2 is not a binary tree. We will check out through our function.

C++ class implementation for tree

// tree node is defined
class tree{    
	public:
		int data;
		tree *left;
		tree *right;
};

C++ function checkBST for implementation

//passing reference of prev
int checkBST(tree* root,int &prev){ 
	//null tree is BST
	if(root==NULL) 
		return 1;
	//doing inorder traversal and checking whether 
	//all tree node data is sorted or not
	if(!(checkBST(root->left,prev))) 
		return 0;
	if(root->data<prev)
		return 0;
	prev=root->data; //update prev value

	return checkBST(root->right,prev);
}

C++ implementation for creating tree nodes

// creating new node
tree* newnode(int data)  
{ 
	tree* node = (tree*)malloc(sizeof(tree)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 

	return(node); 
} 

Main driver function for example1

#include <bits/stdc++.h>
using namespace std;

int main() 
{ 
	//**same tree is builted as shown in example**
	int c,prev=INT_MIN;//prev initialized to INT_MIN
	cout<<"Tree is built like the example 1 aforesaid"<<endl;

	tree *root=newnode(8); 
	root->left= newnode(3); 
	root->right= newnode(10); 
	root->right->right=newnode(14);
	root->right->right->left=newnode(13);
	root->left->left=newnode(1); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(4);
	root->left->right->right=newnode(7);

	cout<<"builting the binary tree like example 1......"<<endl; 
	c=checkBST(root,prev);
	if(c)
		cout<<"This binary tree is binary search tree"<<endl;
	else
		cout<<"This is not a binary search tree";

	return 0; 
} 

Main driver function for example2

#include <bits/stdc++.h>
using namespace std;

int main() 
{ 
	//**same tree is builted as shown in example**
	int c,prev=INT_MIN;//prev initialized to INT_MIN
	cout<<"Tree is built like the example 2 aforesaid"<<endl;

	tree *root=newnode(2); 
	root->left= newnode(7); 
	root->right= newnode(5); 
	root->right->right=newnode(9);
	root->right->right->left=newnode(4);
	root->left->left=newnode(2); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(5);
	root->left->right->right=newnode(11);

	cout<<"builting the binary tree like example 2......"<<endl; 
	c=checkBST(root,prev);
	if(c)
	cout<<"This binary tree is binary search tree"<<endl;
	else
	cout<<"This is not a binary search tree";

	return 0; 
} 

Output 1

Tree is built like the example 1 aforesaid 
builting the binary tree like example 1......
This binary tree is binary search tree

Output 2

Tree is built like the example 2 aforesaid 
builting the binary tree like example 2......
This is not a binary search tree