Home » Interview coding problems/challenges

Count Numbers with unique digits

Count Numbers with unique digits: Here, we are going to learn about the solution to count numbers(x) that can be formed with unique digits, where 0<=x<10^n.
Submitted by Radib Kar, on February 12, 2020

Description:

This is a standard combinatorics problem to count numbers(x) that can be formed with unique digits, where 0<=x<10^ⁿ.

Problem statement:

Given a non-negative integer n, count all numbers with unique digits, x, 0<=x<10^ⁿ.

    Input & output:
    n=2
    Total numbers that can be formed is 91

Explanation with example

    For n =2.
    
    Total numbers = 0 to 102 (excluding) 
    except 11, 22, 33, 44, 55, 66, 77, 88, 99 which has repeated digits.

Problem Solution Approach

• If number of digits is 0, then unique numbers that can be formed is 0
• If number of digits is 1, then unique numbers that can be formed is 10
  0, 1, 2, 3, 4, 5, 6, 7, 8, 9
• If number of digits is 2,
  Then for the first digit (from left), we have 9 choices (excluding 0) [1 to 9]
  And for second digit we have 9 choices (0 to 10 except the previous digit)
  So basically, the number is:
  ij where i=[1,9] and j=[0,9]and i≠j
  So, total number possible are 9*9=81
• If number of digits is 3,
  Then for first digit (from left), we have 9 choices (excluding 0) [1 to 9]
  And for second digit we have 9 choices (0 to 10 except the previous digit)
  And for third digit we have 8 choices (0 to 10 except the previous two digits)
  So basically, the number is:
  ijk where i=[1,9] and j,k=[0,9]and i≠j & j≠k,i
  So, total number possible are 9*9*8=648
  So, if number of digits is i, then the i^th digit will have (10-i+1) choices
  So, we can formulate
  
  

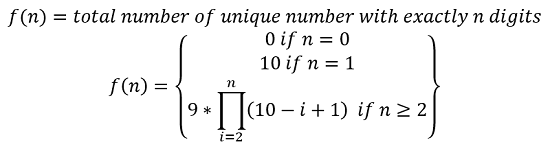
Now this above recursion can be implemented using dynamic programming.

    DP[i] = f(i)=total number of unique number with exactly i digits

    1)  Initialize DP[n+1]  with 0
    2)  DP[0]=0,DP[1]=10,DP[2]=81
    3)  Result = count of total numbers(x) that can be 
        formed with unique digits,where 0<=x<10^n
    4)  Base value of result=91(for n=2)
    5)  for i=3 to n
            DP[i]=DP[i-1]*(10-i+1);
            result=result+DP[i];
        end for
    6)  Return result

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

int countNumbersWithUniqueDigits(int n)
{
    //base cases
    if (n == 0)
        return 0;
    if (n == 1)
        return 10;
    if (n == 2)
        return 91;

    //base value
    long long int DP[n + 1];
    DP[0] = 0;
    DP[1] = 10;
    DP[2] = 81;
    long long int res = 91;

    for (int i = 3; i <= n; i++) {
        //compute f(i)
        DP[i] = DP[i - 1] * (10 - i + 1);
        res += DP[i]; //add f(i)
    }
    //result
    return res;
}

int main()
{
    int n;

    cout << "Enter the number\n";
    cin >> n;

    int ans = countNumbersWithUniqueDigits(n);
    cout << "Total number count is: " << ans << endl;

    return 0;
}

Output

RUN 1:
Enter the number
3
Total number count is: 739

RUN 2:
Enter the number
5
Total number count is: 32491