Home » Interview coding problems/challenges

Highway billboard

Highway billboard: Here, we are going to learn to find maximum profits with some constraints. This can be featured in any interview coding rounds. Submitted by Radib Kar, on February 04, 2020

Description

This is a standard dynamic programing problem of finding maximum profits with some constraints. This can be featured in any interview coding rounds.

Problem statement

Consider a highway of M miles. The task is to place billboards on the highway such that revenue is maximized. The possible sites for billboards are given by number x₁ < x₂ < ... < x_(n-1) < x_n specifying positions in miles measured from one end of the road. If we place a billboard at position x_i, we receive a revenue of r_i > 0. The constraint is that no two billboards can be placed within t miles or less than it.

    Input:
    M=15, n=5
    x[n]= {6,8,12,14,15}
    revenue[n] = {3,6,5,3,5}
    t = 5

    Output:
    11

Explanation with example

So, we have to maximize the revenue by placing the billboards where the gap between any two billboard is t.

Here,

The corresponding distances of the billboards with respect to the origin are,

    x[5]= {6,8,12,14,15}

We can augment the origin, so the augmented array becomes: (no need to augment if origin revenue exists)

    x[6]= {0,6,8,12,14,15}
    t=5

The graphical interpretation of the billboards is like following:

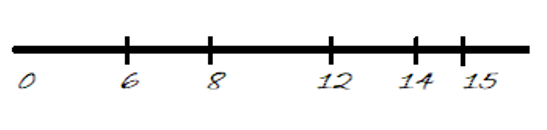
Figure 1: Billboards

The augmented revenue array:

    revenue[6] = {0,3,6,5,3,5}

Now, the brute force approach can be to check all the possible combination of billboards and updating the maximum revenue accumulated from each possible combinations.

Few of such possible combinations can be:

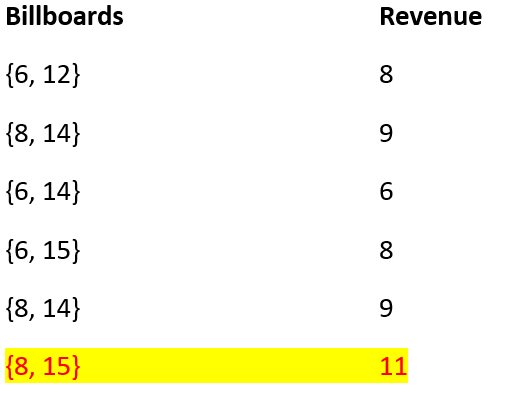
So, maximum revenue that can be collected is 11.

For any billboard b_i we have three choices

1. Don't pick b_i
2. Start from b_i
3. Pick b_i and other billboards accordingly

Say,

    M(i)=maximum revenue upto first i billboards

So,

    M(0)=0
    if bi is not picked, M(i)=M(i-1)
    if billboard placement starts from bi M(i)=r[i]
    If we place bi then need to pace bj where d[i]>d[j]-t such that revenue maximizes
    
    So,
    

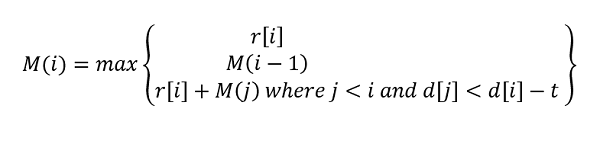
Problem Solution approach

We convert the above recursion to dynamic programing as there will many overlapping sub problems solving the recursion. (Try to generate the recursion tree yourself)

    1) Construct DP[n] for n billboards
        // considering billboard placing starts from it
    2) Fill the array with base value which is r[i] 

    3) for  i=1 to n-1
            // recursion case 1 and 2
            // either not picking ith billboard or starting 
            // from ith billboard which ever is maximum
            dp[i] = max(dp[i-1],dp[i]);
            // recursion case 3
            // picking ith billboard
            for j=0 to i-1
            if(a[j]< a[i]-k)//feasible placing
                dp[i]= max(dp[i],dp[j]+r[i]);
            end for
        end for
        Result is dp[n-1]

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int max(int x, int y)
{
    return (x > y) ? x : y;
}

int billboard(vector<int> a, vector<int> r, int n, int k)
{
    int dp[n];

    for (int i = 0; i < n; i++)
        dp[i] = r[i];

    //base value
    dp[0] = r[0];
    for (int i = 1; i < n; i++) {
        //first two recursion case
        int mxn = max(dp[i - 1], dp[i]);
        //picking ith billboard, third recursion case
        for (int j = 0; j < i; j++) {
            if (a[j] < a[i] - k)
                mxn = max(mxn, dp[j] + r[i]);
        }
        dp[i] = mxn;
    }

    return dp[n - 1];
}

int main()
{
    int n, k, item, m;

    cout << "Enter highway length:\n";
    cin >> m;
    cout << "Enter number of billboards\n";
    cin >> n;
    cout << "Enter minimum distance between any two billboards\n";
    cin >> k;

    vector<int> a;
    vector<int> r;

    cout << "Enter billboard distances one by one from origin\n";
    for (int i = 0; i < n; i++) {
        cin >> item;
        a.push_back(item);
    }
    cout << "Enter revenues for the respective billboards\n";
    for (int i = 0; i < n; i++) {
        cin >> item;
        r.push_back(item);
    }

    if (a[0] == 0) {
        a.insert(a.begin(), 0);
        r.insert(r.begin(), 0);
        n = n + 1;
    }

    cout << "Maximum revenue that can be collected is: " << billboard(a, r, n, k) << endl;

    return 0;
}

Output

RUN 1:
Enter highway length:
20
Enter number of billboards
5
Enter minimum distance between any two billboards
5
Enter billboard distances one by one from origin
3 7 12 13 14
Enter revenues for the respective billboards
15 10 1 6 2
Maximum revenue that can be collected is: 21

RUN 2:
Enter highway length:
15
Enter number of billboards
5
Enter minimum distance between any two billboards
5
Enter billboard distances one by one from origin
6 8 12 14 15
Enter revenues for the respective billboards
3 6 5 3 5
Maximum revenue that can be collected is: 11