Home » Interview coding problems/challenges

Diameter of Binary Tree

In this article, we are going to see how to find diameter of a tree? This is a very popular problem to be asked and has already been featured in Amazon, MakeMyTrip, Microsoft, Oracle, VMWare, Oyo rooms etc. Submitted by Radib Kar, on February 11, 2019

Problem statement

Given a Binary Tree, find diameter of it. The diameter of a tree is the number of nodes on the longest path between two leaves in the tree.

Example

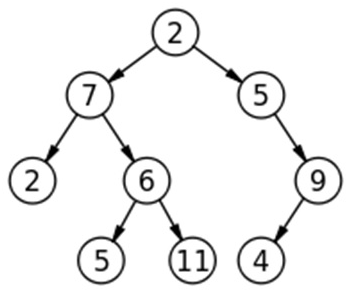
    For the above tree:

    Diameter is 7

    Longest paths:
    11->6->7->2->5->.9->4
    5->6->7->2->5->9->4
    
    Both have 7 nodes

Solution Approach

Diameter of a tree

Diameter of a tree is number of nodes on the longest path between two leaves of tree.

Now the fact is the longest path always passes through the root.

In fact no of nodes=height of left subtree (there is the source/destination leaf node) + height of right subtree(there is the destination/source leaf node) + 1(for root)

So actually the solution depends on finding the height of each subtree.

Finding height of each subtree can be done using recursion or level order traversal. However, I prefer level order traversal (BFS rocks!)

Algorithm

Diameter=height of left subtree + height of right subtree+1

Pre-requisite:

A Queue q for level-order traversal, input binary tree, function to calculate height of subtrees

FUNCTION height (root)
1.  Set h=1;
    EnQueue (q, root);
    EnQueue (q, NULL);
    While(q is not empty)
        temp=DeQueue(q) 	
        IF(temp is NULL)
            IF(q is not empty)
                EnQueue (q, NULL);
                h++; //increment height as this is the end of the processed level
            End IF
        ELSE
            IF(temp->left)
                EnQueue (temp->left);
            IF(temp->right)
                EnQueue (temp->right);
            End IF-ELSE
    End While

2.  Return h; //height of the tree
End FUNCTION

FUNCTION diameter (root)
	Return height (root->left) +height(root->right) +1;
End FUNCTION

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class TreeNode{    
	public:
	int data;
	TreeNode *left;
	TreeNode *right;
};

// creating new node for tree
TreeNode* newnode(int data)  
{ 
	TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 

	return(node); 
} 

int height(TreeNode* node){
	int h=1;	
	queue<TreeNode*> q;
	Node* temp;
	
	q.push(node);
	q.push(NULL);
	while(!q.empty()){
		temp=q.front();
		q.pop();
		if(!temp){
			if(!q.empty()){
				q.push(NULL);
				h++;
			}
		}
		else{
			if(temp->left)
				q.push(temp->left);
			if(temp->right)
				q.push(temp->right);
		}
	}
	return h;
}

int diameter(TreeNode* node)
{
	if(node==NULL)
		return 0;
	return height(node->left)+height(node->right)+1;
}

int main() { 
	//**same tree is builted as shown in example**
	int k;
	cout<<"same tree is built as shown in example\n";
	
	TreeNode *root=newnode(2); 
	
	root->left= newnode(7); 
	root->right= newnode(5); 
	root->right->right=newnode(9);
	root->right->right->left=newnode(4);
	root->left->left=newnode(2); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(5);
	root->left->right->right=newnode(11);

	cout<<"Diameter of the tree is:\n"<<diameter(root);

	return 0; 
} 

Output

same tree is built as shown in example
Diameter of the tree is:
7 

Explanation with example

For our example tree
Calculating height of left-subtree

Root=2;
Root->left=7
Root->right=5
------------------------------------------

height(7)
h=1
root=7
Push 7
Push NULL
Queue status:
7, NULL

1st iteration
Queue not empty
Queue front is 7
Pop 7
Push: 7->left(2) & 7->right(6)
Queue status: NULL, 2, 6
------------------------------------------

2nd iteration
Queue not empty
Queue front is NULL
Pop NULL
Increment h; h=2
Push: NULL
Queue status: 2, 6, NULL
------------------------------------------

3rd iteration
Queue not empty
Queue front is 2
Pop 2
Push: Nothing ( 2->left (NULL) and 7->right (NULL) 
Queue status:  6, NULL
------------------------------------------

4th iteration
Queue not empty
Queue front is 6
Pop 6
Push: 6->left (5) 6->right (11) 
Queue status: NULL, 5,11
------------------------------------------

5th iteration
Queue not empty
Queue front is NULL
Pop NULL
Increment h//h=3

Push: NULL
Queue status: 5, 11, NULL
------------------------------------------

6th iteration
Queue not empty
Queue front is 5
Pop 5
Push: Nothing (5->left is NULL, 5->right is NULL)
Queue status: 11, NULL
------------------------------------------

7th iteration
Queue not empty
Queue front is 11
Pop 11
Push: Nothing (11->left is NULL, 11->right is NULL)
Queue status: NULL
------------------------------------------

8th iteration
Queue not empty
Queue front is NULL
Pop NULL
Queue is empty
So no more pushing NULL
------------------------------------------

Queue is empty, hence end
Thus height of left subtree is 3

Same way we can proceed to calculate right subtree height which is also 3
Thus diameter of the tree is 3+3+1=7