Home »
Interview coding problems/challenges
Largest Independent Set Problem
Here, we are going to learn the solution of the largest independent set problem using dynamic programming.
Submitted by Souvik Saha, on June 25, 2020
Problem statement
Given a tree, you have to find out the largest independent set. Independent elements are those that don’t have any common edges. Print the length of the largest independent set.
T Test case
T no. of input string will be given to you.
E.g.
2
 Output:
Print the length of the largest Independent set.
Output:
Print the length of the largest Independent set.
Example
T=2
Input:
 Output:
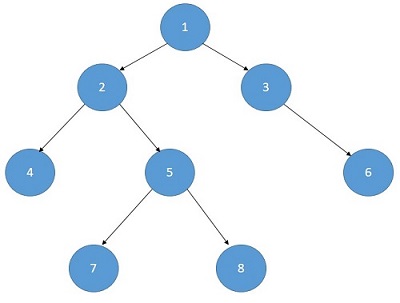
5 ( 1,4,7,8,6)
Input:
Output:
5 ( 1,4,7,8,6)
Input:
 Output:
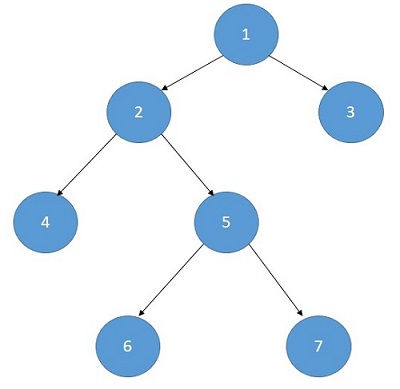
4 (3,2,6,7)
Output:
4 (3,2,6,7)
Explanation with example
To find out the length of the independent set we have to consider every node in our consideration.
- A node with its grandchildren are in the set
- The child nodes are in the set.
Independent set of node(x) = max (1+independent set of its grandchildren,independent set of its children)
Example
 In that case,
Independent set of the node(1) =
max ( independent set of node(4), node(5) and node(6)+1 ,
independent set of the node(2)and node(3)
In that case,
Independent set of the node(1) =
max ( independent set of node(4), node(5) and node(6)+1 ,
independent set of the node(2)and node(3)
Problem Solution:
Recursive algorithm:
Function(Node):
if(node==NULL)
return 0
excluding_the_node=Function(node->left)+Function(node->right)
including_the_node=1
if(node->left)
including_the_node+=Function(node->left->left)+Function(node->left->right)
if(node->right)
including_the_node+=Function(node->right->left)+Function(node->right->right)
return max(including_the_node,excluding_the_node)
DP conversion:
Function(Node):
if(node==NULL)
return 0
if(vis[node])
return vis[node]
excluding_the_node=Function(node->left)+Function(node->right)
including_the_node=1
if(node->left)
including_the_node+=Function(node->left->left)+Function(node->left->right)
if(node->right)
including_the_node+=Function(node->right->left)+Function(node->right->right)
return vis[node]=max(including_the_node,excluding_the_node)
C++ Implementation
#include <bits/stdc++.h>
using namespace std;
struct tree {
int val, value;
tree* left;
tree* right;
};
struct tree* make_node(int x)
{
tree* t = new tree;
t->val = x;
t->value = 0;
t->left = t->right = NULL;
return t;
}
int set_count(tree* t)
{
if (t == NULL) {
return 0;
}
if (t->value) {
return t->value;
}
int excluding = set_count(t->left) + set_count(t->right);
int including = 1;
if (t->left)
including += set_count(t->left->left) + set_count(t->left->right);
if (t->right)
including += set_count(t->right->left) + set_count(t->right->right);
return max(excluding, including);
}
int main()
{
tree* t = NULL;
t = make_node(10);
t->left = make_node(20);
t->right = make_node(30);
t->left->left = make_node(40);
t->left->right = make_node(50);
t->right->right = make_node(60);
t->right->left = make_node(90);
t->left->right->left = make_node(70);
t->left->right->right = make_node(80);
cout << "Max set count : " << set_count(t) << endl;
return 0;
}
Output
Max set count : 6
Advertisement
Advertisement